CSAPP5

优化编译器的能力和局限性

指向同一内存位置

编译器优化程序性能的能力是有限的。编译器可以执行一些基本的优化，如循环展开、常量传播和死代码消除

但它们无法理解程序的高层次语义和上下文。因此，编译器可能无法识别某些优化机会，尤其是在复杂的代码结构中

此外，编译器优化通常是基于静态分析，而动态行为（如运行时数据分布）可能会影响性能，这些信息在编译时是不可用的。

比如下面两个过程

void twiddle1(long *xp, long *yp)
{
    *xp += *yp;
    *xp += *yp;
}

void twiddle2(long *xp, long *yp)
{
    *xp += 2* *yp;
}

乍一看，这两个过程似乎有相同的行为。它们都是将存储在由指针 yp 指示的位置处的值两次加到指针 xp 指示的位置处的值

另一方面，函数 twiddle2 效率更高一些。它只要求 3 次内存引用（读 xp, 读 yp, 写 *xp）

而 twiddle1 需要 6 次（2 次读 xp, 2 次读 yp, 2 次写 *xp）

因此，如果要编译器编译过程 twiddle1，我们会认为基于 twiddle2 执行的计算能产生更有效的代码

不过，考虑 xp 等于 yp 的情况

此时，函数 twiddle1 会执行下面的计算

1 2	xp += xp; /* Double value at xp / xp += xp; / Double value at xp */

结果是 xp 的值增加 4 倍。另一方面，函数 twiddle2 会执行下面的计算

1	xp += 2 xp; / Triple value at xp */

结果是 xp 的值增加 3 倍

编译器不知道 twiddle1 会如何被调用，因此它必须假设参数 xp 和 yp 可能会相等

因此，它不能产生 twiddle2 风格的代码作为 twiddle1 的优化版本

这也说明了，如果编译器不能确定两个指针是否可能指向同一内存位置，它就不能对涉及这些指针的代码进行某些优化

函数调用

第二个妨碍优化的因素是函数调用

long f();

long func1() {
    return f() + f() + f() + f();
}

long func2() {
    return 4*f();
}

最初看上去两个过程计算的都是相同的结果

但是 func2 只调用 f 一次，而 func1 调用 f 四次

但考虑这样的 f

long counter = 0;

long f() {
    return counter++;
}

这个函数有个副作用——它修改了全局程序状态的一部分。改变调用它的次数会改变程序的行为

特别地，假设开始时全局变量 counter 都设置为 0，对 func1 的调用会返回 0 + 1 + 2 + 3 = 6，而对 func2 的调用会返回 4 · 0 = 0

大多数编译器不会试图判断一个函数是否没有副作用，如果没有，就可能被优化成像 func2 中的样子。相反，编译器会假设最糟的情况，并保持所有的函数调用不变

表示函数性能

每元素的周期数（CPE）作为表示程序性能的方法

处理器活动的顺序是由时钟控制的，时钟提供了某个频率的规律信号

通常用千兆赫 .兹(GHz), 即十亿周期每秒来表示

例如，当表明一个系统有“4GHz”处理器，这表示处理器时钟运行频率为每秒\(4\times 10^{9}\)个周期。

每个时钟周期的时间是时钟频率的倒数。通常是以纳秒（nanosecond, 1 纳秒等于 \(10^{-9}\) 秒）或皮秒（picosecond, 1 皮秒等于 \(10^{-12}\)秒）为单位的

从程序员的角度来看，用时钟周期来表示度量标准要比用纳秒或皮秒来表示有帮助得多

这样一个过程所需要的时间可以用一个常数加上一个与被处理元素个数成正比的因子来描述

做出周期-元素图，图中每个点表示处理 n 个元素所需的周期数，假设一个过程的周期-元素图是一条直线 \[ T(n) = T_0 + CPE \times n \] 则这条直线的斜率 CPE 表示每处理一个元素所需的平均周期数

其中 T0 是一个常数，表示过程的固定开销（如函数调用开销）

一般认为 CPE 越低，程序越快

练习 5.2

n 为 0、1 或 2 时，版本 1 最快。 n 为 3 到 7 之间的整数时，版本 2 最快。 n 大于或等于 8 时，版本 3 最快。

未经优化的代码是从C语言代码到机器代码的直接翻译，通常效率明显较低。简单地使用命令行选项“-O1”，就会进行一些基本的优化

正如可以看到的，程序员不需要做什么，就会显著地提高程序性能 —— 超过两个数量级

通常，养成至少使用这个级别优化的习惯是很好的。（使用-Og优化级别能得到相似的性能结果。

考虑最初始的函数，接下来会对这个函数进行若干优化

在一个具有 Intel Core i7 Haswell 的处理器上测量相关的 CPE 值

void combine1(vec_ptr v, data_t *dest){
    long i;
    
    *dest = IDENT;
    for(int i = 0; i < vec_length(v);i++){
        data_t val;
        get_vec_element(v,i,&val);        
        *dest = *dest OP val;
    }
}

实验显示32位整数操作和64位整数操作有相同的性能，除了涉及除法操作的版本

同样，对于操作单精度和双精度浮点数的版本，性能也相似，因此在表中只给出整数和浮点数各自的结果

未经优化的代码是从C语言代码到机器代码的直接翻译，通常效率明显较低。简单地使用命令行选项“-O1”，就会进行一些基本的优化

代码移动

可以看到，调用了函数 vec_lenth 作为测试条件

但这个函数每次调用时都要计算向量的长度，这在循环中是低效的

相当于每次又遍历了一次向量，这会使得整体复杂度从 \(O(n)\) 变成 \(O(n^2)\)

所以做出优化版本

void combine2(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    
    *dest = IDENT;
    for(int i = 0; i < length;i++){
        data_t val;
        get_vec_element(v,i,&val);        
        *dest = *dest OP val;
    }
}

可以看到，将不变的计算移出循环体可以显著地提高程序性能

这种优化称为代码移动（code motion）

即识别要执行多次但结果不变的计算，并将这些计算移到循环之外

考虑下面这两个函数

/* Convert string to lowercase: slow */
void lower1(char *s)
{
    long i;

    for (i = 0; i < strlen(s); i++)
        if (s[i] >= 'A' && s[i] <= 'Z')
            s[i] -= ('A' - 'a');

}

/* Convert string to lowercase: faster */
void lower2(char *s)
{
    long i;
    long len = strlen(s);

    for (i = 0; i < len; i++)
        if (s[i] >= 'A' && s[i] <= 'Z')
            s[i] -= ('A' - 'a');

}

/* Sample implementation of library function strlen */
/* Compute length of string */
size_t strlen(const char *s)
{
    long length = 0;
    while (*s != '\0') {
        s++;
        length++;
    }
    return length;
}

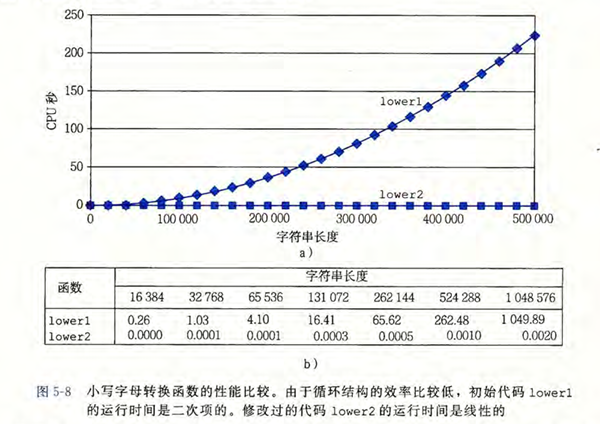
可以看到，仅仅是将对 strlen 的调用移出循环体，就能显著地提高程序性能

但是编译器不能自动执行这种优化，因为它不能确定 strlen 函数是否有副作用

练习 5.3

根据题目给出的代码片段和假设条件（\(x = 10\)，\(y = 100\)），我们可以计算出各个函数被调用的次数。

首先，min(10, 100) = 10，max(10, 100) = 100。循环迭代的次数为 \(100 - 10 = 90\) 次。

分析过程：

代码片段 A：
- min：在 for 循环初始化部分调用一次。次数 = 1。
- max：在循环条件 i < max(x, y) 中。循环成功执行 90 次，条件判定为真 90 次；循环结束前最后一次判定为假，也调用了一次。次数 = 90 + 1 = 91。
- incr：在每次循环体执行完后调用。次数 = 90。
- square：在循环体内每次调用。次数 = 90。
代码片段 B：
- max：在 for 循环初始化部分调用一次。次数 = 1。
- min：在循环条件 i >= min(x, y) 中。循环成功执行 90 次，条件判定为真 90 次；最后一次判定为假时也调用一次。次数 = 90 + 1 = 91。
- incr：每次循环体执行完后调用。次数 = 90。
- square：循环体内每次调用。次数 = 90。
代码片段 C：
- min：在循环外初始化 low 时调用一次。次数 = 1。
- max：在循环外初始化 high 时调用一次。次数 = 1。
- incr：循环执行 90 次，末尾调用 90 次。次数 = 90。
- square：循环体内调用 90 次。次数 = 90。

代码	min	max	incr	square
A.	1	91	90	90
B.	91	1	90	90
C.	1	1	90	90

减少过程调用

每次循环迭代都会调用get_vec_element 来获取下一个向量元素

对每个向量引用，这个函数要把向量索引 i 与循环边界做比较，很明显会造成低效率

作为替代，假设为我们的抽象数据类型增加一个函数 get_vec_start，返回起始地址

data_t* get_vec_start(vec_ptr v){
    return v->data;
}

void combine3(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    
    *dest = IDENT;
    for(int i = 0; i < length;i++){
        data_t val = data[i];        
        *dest = *dest OP val;
    }
}

但是实际上性能并没有显著提升，事实上，整数求和的 CPE 略有增加即性能下降

消除不必要的内存引用

combine3 的代码将合并运算计算的值累积在指针 dest 指定的位置。通过检查编译出来的为内循环产生的汇编代码，可以看出这个属性。在此我们给出数据类型为 double，合并运算为乘法的 x86-64 代码：

#Inner loop of combine3.  data_t = double, OP = *
#dest in %rbx, data+i in %rdx, data+length in %rax
.L17:                            loop:
    vmovsd  (%rbx), %xmm0        #Read product from dest
    vmulsd  (%rdx), %xmm0, %xmm0  #Multiply product by data[i]
    vmovsd  %xmm0, (%rbx)        #Store product at dest
    addq    $8, %rdx             #Increment data+i
    cmpq    %rax, %rdx           #Compare to data+length
    jne     .L17                 #If !=, goto loop

在这段循环代码中，我们看到，指针 dest 的地址存放在寄存器 %rbx 中，它还改变了代码，将第 i 个数据元素的指针保存在寄存器 %rdx 中，注释中显示为 data+i。每次迭代，这个指针都加 8

循环终止操作通过比较这个指针与保存在寄存器 %rax 中的数值来判断

我们可以看到每次迭代时，累积变量的数值都要从内存读出再写入到内存

这样的读写很浪费，因为每次迭代开始时从 dest 读出的值就是上次迭代最后写入的值。

我们能够消除这种不必要的内存读写，按照 combine4 所示的方式重写代码

引入一个临时变量 acc，它在循环中用来累积计算出来的值

只有在循环完成之后结果才存放在 dest 中。正如下面的汇编代码所示，编译器现在可以用寄存器 %xmm0 来保存

void combine4(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    for(int i = 0; i < length;i++){
        data_t val = data[i];        
        acc = acc OP val;
    }
    *dest = acc;
}

在这个版本中，内循环的汇编代码如下所示：

#Inner loop of combine4.  data_t = double, OP = *
#acc in %xmm0, data+i in %rdx, data+length in %rax
.L19:                            loop:
    vmulsd  (%rdx), %xmm0, %xmm0 # Multiply acc by data[i]
    addq    $8, %rdx             # Increment data+i
    cmpq    %rax, %rdx           #Compare to data+length   
    jne     .L19                 #If !=, goto loop

程序性能有了显著的提高

当然，我们说明 combine3 和 combine4 之间差别的例子是人为设计的。有人会说 combine4 的行为更加符合函数描述的意图，但是编译器并不能理解这些意图

在编译 combine3 时，编译器不能确定 dest 是否在循环中被其他代码修改过

保守的方式就是假设 dest 可能在每次迭代中被修改，因此每次都必须从内存中读取它的值

练习题 5.4 当用命令行选项 “-O2” 的 GCC 来编译 combine3 时，得到的代码 CPE 性能远好于使用 -O1 时的：

函数	方法	整数 (+)	整数 (*)	浮点数 (+)	浮点数 (*)
combine3	用 -O1 编译	7.17	9.02	9.02	11.03
combine3	用 -O2 编译	1.60	3.01	3.01	5.01
combine4	累积在临时变量中	1.27	3.01	3.01	5.01

由此得到的性能与 combine4 相当，不过对于整数求和的情况除外，虽然性能已经得到了显著的提高，但还是低于 combine4。在检查编译器产生的汇编代码时，我们发现对内循环的一个有趣的变化：

#Inner loop of combine3.  data_t = double, OP = *.  Compiled -O2
#dest in %rbx, data+i in %rdx, data+length in %rax
#Accumulated product in %xmm0
.L22:                            loop:
    vmulsd  (%rdx), %xmm0, %xmm0  Multiply product by data[i]
    addq    $8, %rdx             #Increment data+i
    cmpq    %rax, %rdx           #Compare to data+length
    vmovsd  %xmm0, (%rbx)        #Store product at dest
    jne     .L22                 #If !=, goto loop

把上面的代码与用优化等级 1 产生的代码进行比较：

#Inner loop of combine3.  data_t = double, OP = *.  Compiled -O1
#dest in %rbx, data+i in %rdx, data+length in %rax
.L17:                            loop:
    vmovsd  (%rbx), %xmm0        #Read product from dest
    vmulsd  (%rdx), %xmm0, %xmm0  #Multiply product by data[i]
    vmovsd  %xmm0, (%rbx)        #Store product at dest
    addq    $8, %rdx             #Increment data+i
    cmpq    %rax, %rdx           #Compare to data+length
    jne     .L17                 #If !=, goto loop

我们看到，除了指令顺序有些不同，唯一的区别就是使用更优化的版本不含有 vmovsd 指令，它实现的是从 dest 指定的位置读数据 A. 寄存器 %xmm0 的角色在两个循环中有什么不同？ B. 这个更优化的版本忠实地实现了 combine3 的 C 语言代码吗（包括在 dest 和向量数据之间使用内存别名的时候）？ C. 解释为什么这个优化保持了期望的行为，或者给出一个例子说明它产生了与使用较少优化的代码不同的结果。

解答：

A. 在 -O1 编译的代码中，寄存器 %xmm0 仅作为一个临时变量，用于在单次迭代中暂存从内存读出的 dest 值。在 -O2 编译的代码中，寄存器 %xmm0 扮演了累加器（accumulator）的角色，它在多次迭代之间保存并传递乘积的中间结果，从而省去了每轮迭代开始时重复从内存读取 dest 的操作。

B. 这个更优化的版本忠实地实现了 combine3 的语义。即使存在内存别名（即 dest 指向 data 数组中的某个元素），该版本的行为也与原始 C 代码逻辑一致。

C. 该优化之所以能保持期望的行为，是因为它虽然省略了从 dest 读数据的操作，但仍然在每次迭代的末尾执行了 vmovsd %xmm0, (%rbx)，将计算出的新值写回到 dest 指向的内存位置。 如果不存在别名：减少一次多余的内存读取显然不影响结果。 * 如果存在别名（例如 dest 指向 data[i]）：在 -O1 中，程序会先后读取 *dest 和 data[i]（读到同一个地址的同一个值）。在 -O2 中，程序使用寄存器里已有的上一次迭代的结果，并读取一次内存中的 data[i]。由于上一次迭代已经通过写操作更新了内存，寄存器里的值和内存里的值是一致的，因此计算出的结果相同。由于每轮迭代都确保了内存被及时更新，后续迭代如果访问到被别名化的 data 元素，依然能读到正确更新后的值。所以此优化在逻辑上是安全的。

现代处理器

当一系列操作必须按照严格顺序执行时，就会遇到延迟界限（latency bound) 因为在下一条指令开始之前，这条指令必须结束

当代码中的数据相关限制了处理器利用指令级并行的能力时，延迟界限能够限制程序性能。吞吐量界限（throughput tcnmd)刻画了处理器功能单元的原始计算能力

ICU从指令高速缓存中读取指令，采用了分支预测技术来猜测程序的控制流

处理器猜测是否会选择分支，还预测目标分支的地址，使用投机执行的技术来执行预测的指令路径

在一个典型的x86实现中，一条只对寄存器操作的指令

1	addq %rax, %rbx

被转化为另一个操作

1	addq %rax, 8(%rbx)

这条指令会被译码成为三个操作

读取寄存器 %rbx 的值
将寄存器 %rax 的值加到内存地址 8 + (%rbx) 处
将结果写回到内存地址 8 + (%rbx) 处

使用投机执行技术对操作求值，但是最终结果不会存放在程序寄存器或数据内存中，直到处理器能确定应该实际执行这些指令

控制操作数在执行单元间传送的最常见的机制称为寄存器重命名（register renaming)

当一条更新寄存器r的指令译码时，产生标记 t，得到一个指向该操作结果的唯一的标识符，(r,t) 被加入到一张表中，该表维护寄存器名到物理寄存器的映射

当随后以寄存器 r 作为操作数的指令译码时，发送到执行单元的操作会包含 t 作为操作数源的值。当某个执行单元完成第一个操作时，会生成一个结果(v，t)ÿ 指明标记为 t 的操作产生值 v

通过这种机制，值可以从一个操作直接转发到另一个操作，而不是写到寄存器文件再读出来，使得第二个操作能够在第一个操作完成后尽快开始。重命名表只包含关于有未进行写操作的寄存器条目

处理器使用乱序执行（out-of-order execution) 技术来提高指令级并行性处理器维护一个保留站（reservation station) 列表，保存已译码但尚未执行的指令

练习 5.5

对于次数 n，循环从 i = 1 执行到 i = degree（即 n），总共执行 n 次。每次循环包含：

1 次加法：result += …
2 次乘法：a[i] * xpwr 和 x * xpwr 因此，总共执行 n 次加法和 2n 次乘法

性能受限于数据流中的关键路径。代码中有两个主要的更新操作：

result = result + (a[i] * xpwr)
xpwr = x * xpwr 这两个操作在迭代之间形成了两个独立的数据相关链。

result 链：当前的 result 取决于前一次迭代的 result 加上一个乘积。关键路径上是一个浮点加法（假设延迟为 3 个时钟周期）。
xpwr 链：当前的 xpwr 取决于前一次迭代的 xpwr 乘以 x。关键路径上是一个浮点乘法（假设延迟为 5 个时钟周期）。由于处理器可以并行执行不相关的指令，这两个链是并行运行的。性能由最慢的链（瓶颈）决定。在这个参考机上，浮点乘法的延迟是 5.00 个时钟周期，因此 CPE 为 5.00

练习 5.6

对于次数 n，循环从 i = degree - 1 执行到 i = 0，总共执行 n 次。每次循环包含：

1 次加法：a[i] + …
1 次乘法：x * result 因此，总共执行 n 次加法和 n 次乘法。

在 Horner 法的代码中，每一轮迭代的计算公式为：result = a[i] + (x * result)。这意味着当前迭代的 result 值必须等待前一次迭代的 result 计算完成。具体的依赖路径是：先进行一次乘法（x * result），然后进行一次加法（+ a[i]）。关键路径的延迟 = 乘法延迟 + 加法延迟。如果浮点乘法延迟为 5 个周期，浮点加法延迟为 3 个周期，总延迟就是 5 + 3 = 8.00 个周期。这解释了为什么 CPE 等于 8.00

虽然 poly (5.5) 的操作总数更多（2n 次乘法），但它具有更好的指令级并行性（ILP）。它的两个更新链（result 和 xpwr）是独立的，处理器可以同时处理它们。性能只被其中最长的单个操作延迟（乘法，5.00）限制。而 polyh (5.6) 虽然操作更少，但它的计算是严格串行的。每一次迭代都必须等待前一次迭代的“乘法+加法”完整结果，导致这两项操作的延迟累加在一起（5 + 3 = 8.00），无法通过并行化来隐藏延迟。因此，即使运算量更小，polyh 反而运行得更慢

循环展开

循环展开是一种程序变换，通过增加每次迭代计算的元素的数量，减少循环的迭代次数

假设我们有一个简单的向量求和函数，原始代码如下：

1
2
3

for (i = 0; i < n; i++) {
    acc = acc OP data[i];
}

如果我们进行 2 级展开 (2x1 Unrolling)，代码会变成：

int limit = n - 1;
for (i = 0; i < limit; i += 2) {
    acc = (acc OP data[i]) OP data[i+1]; // 一次循环处理两个元素
}
// 处理剩余的元素 (n为奇数的情况)
for (; i < n; i++) {
    acc = acc OP data[i];
}

主要优势如下

减少循环开销 (Reduce Overhead)： 每次循环都要执行：i++（增加索引）、i < n（条件判断）和 jne（跳转指令）。展开后，这些控制指令的执行总次数减少了（例如 2 级展开减少了一半，k 级展开减少了 \(1/k\)）。
提高指令级并行度 (ILP)： 在一个迭代中放入更多独立的操作，可以帮助处理器更有效地调度执行单元。
辅助进一步优化： 展开后的代码为编译器提供了更大的空间来应用其他优化，例如重新结合变换 (Reassociation Transformation) 或使用多个累积变量。

由于数组长度 \(n\) 不一定能被展开因子 \(k\) 整除，循环展开必须包含处理“尾部”元素的逻辑。

方法一： 在主循环之后增加一个简单的循环处理剩下的 \(n \pmod k\) 个元素（如上例）。
方法二： 先处理前 \(n \pmod k\) 个元素，然后再进入展开后的主循环

简单的 \(k \times 1\) 展开（即虽然展开了循环，但仍使用同一个累积变量 acc）往往不能突破延迟界限。

*即使循环展开了，计算仍然是串行的。例如 acc = (acc OP data[i]) OP data[i+1]。计算第二个 OP 必须等待第一个 OP 完成

为了真正突破延迟界限，循环展开通常配合以下技术使用

多累积变量 (\(k \times m\) 展开)： 使用多个独立的累加器（如 acc0, acc1），让 CPU 的多个执行单元同时工作。
- 示例： acc0 = acc0 OP data[i]; acc1 = acc1 OP data[i+1];
重新结合变换 (Reassociation)： 改变计算顺序，打破依赖链。
- 示例： acc = acc OP (data[i] OP data[i+1]); 这里 (data[i] OP data[i+1]) 的计算不依赖于之前的 acc，可以提前并行执行。

尽管循环展开很强大，但不能无限展开：

代码膨胀 (Code Bloat)： 二进制文件变大，可能导致指令高速缓存 (Instruction Cache) 命中率下降，反而变慢
寄存器压力 (Register Pressure)： 如果展开级数过多或使用了过多的临时累积变量，超出了寄存器数量，会导致变量溢出到内存（Spilling），性能剧降
可读性下降： 源码会变得复杂难懂（除非交给编译器自动处理）

所以可以继续优化combine代码

combine5 是 \(2\times 1\) 版本

conbine6 是 \(2\times 2\) 版本

conbine7 是重新结合变换

void combine5(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    int limit = length - 1;
    for(i = 0; i < limit; i += 2){
        data_t val0 = data[i];
        data_t val1 = data[i+1];        
        acc = (acc OP val0) OP val1;
    }
    //处理剩余元素
    for(; i < length; i++){
        data_t val = data[i];
        acc = acc OP val;
    }
    *dest = acc;
}

void combine6(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;
    
    int limit = length - 1;
    for(i = 0; i < limit; i += 2){
        data_t val0 = data[i];
        data_t val1 = data[i+1];        
        acc0 = acc0 OP val0;
        acc1 = acc1 OP val1;
    }
    //处理剩余元素
    for(; i < length; i++){
        data_t val = data[i];
        acc0 = acc0 OP val;
    }
    *dest = acc0 OP acc1;
}

void combine7(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;
    
    int limit = length - 1;
    for(i = 0; i < limit; i += 2){
        data_t val0 = data[i];
        data_t val1 = data[i+1];        
        acc0 = acc0 OP val0;
        acc1 = acc1 OP val1;
    }
    //处理剩余元素
    for(; i < length; i++){
        data_t val = data[i];
        acc0 = acc0 OP val;
    }
    *dest = acc0 OP acc1;
}

循环展开的 \(k\times m\) 的意思是

\(k\) 表示循环展开的级数，即每次迭代处理的元素数量
\(m\) 表示使用的独立累积变量的数量

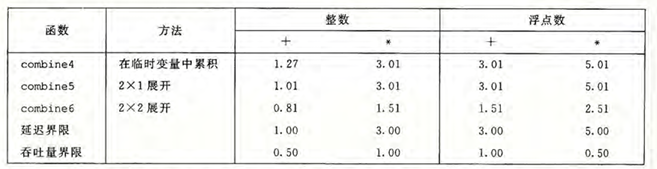
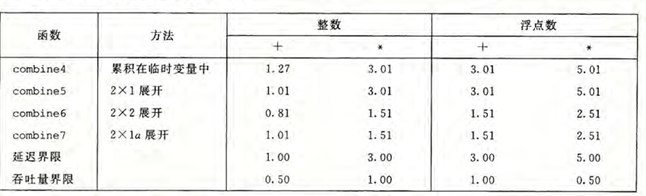
整数加的性能几乎与使用 \(k\times 1\)展开的版本（combines)的性能相同，而其他三种情况则与使用并行累积变量的版本（combines)相同，是 \(k\times 1\) 扩展的性能的两倍。这些情况已经突破了延迟界限造成的限制

在执行重新结合变换时，又一次改变向量元素合并的顺序。

对于整数加法和乘法，这些运算是可结合的，这表示这种重新变换顺序对结果没有影响。

对于浮点数情况，必须再次评估这种重新结合是否有可能严重影响结果

我们会说对大多数应用来说，这种差别不重要

一些限制因素

在程序的数据流图中，关键路径是指最长的指令依赖链。

如果一条指令的结果是下一条指令的输入（数据相关），那么这两条指令必须串行执行。

如果某条依赖链上的所有操作延迟之和为 \(T\)，那么无论处理器有多少并行资源，执行完这条链至少需要 \(T\) 个时钟周期。

这是由于代码的逻辑依赖决定的性能极限。

功能单元与吞吐量下界是由处理器硬件资源的数量决定的性能极限。

执行时间下界 = \(N \cdot I / C\) * \(N\)：程序中某种运算的总次数（如总共有 1000 次加法）。 * \(I\)（发射时间，Issue Time）：同一个功能单元两次起始运算之间的最小周期数（对于流水线化的现代 CPU，通常为 1）。 * \(C\)（容量，Capacity）：能够执行该种运算的功能单元数量。

即使程序中完全没有数据依赖，所有运算都能并行，你仍然会受限于“搬砖的人手不够”。 * 例子：如果有 100 个加法任务（\(N=100\)），CPU 只有 2 个加法器（\(C=2\)），每个周期能开始一次新加法（\(I=1\)），那么最快也需要 \(100 / 2 = 50\) 个周期。

这是由于硬件的物理资源决定的性能极限。

延迟界限：因为你要一步步算，所以快不了。
吞吐量界限：因为硬件只有这么多，所以快不了。

优化程序的目标通常就是：通过循环展开或重新结合等技术，打破关键路径的依赖，使性能从受限于“延迟界限”转向受限于“吞吐量界限”

寄存器溢出

当程序需要的临时值（如累积变量、展开后的中间结果）数量超过了处理器可用的物理寄存器数量时，就会发生寄存器溢出。

编译器被迫将多出来的变量存放在内存（通常是栈帧）中。

一旦发生溢出，原本通过寄存器进行的快速访问就变成了慢速的内存读写。这会导致程序的 CPE（每元素周期数）显著增加。

这是循环展开的一个负面限制。虽然增加展开级数能减少循环开销并提高并行度，但如果级数过多导致寄存器不够用，性能反而会急剧下降。

分支预测和预测错误处罚

现代处理器使用流水线处理指令。为了不让流水线因等待分支结果（如 if 语句）而停顿，处理器会猜测分支的方向并“投机执行”。

如果处理器猜错了（分支预测错误），它必须丢弃所有投机执行的结果，清空流水线，并从正确的位置重新开始取指。

预测错误的处罚通常非常沉重，可能导致约 15 到 30 个时钟周期的浪费，这在高性能循环中是致命的。

不要过分关心可预测分支

现代处理器的分支预测器非常强大，对于具有规律性模式的分支（例如循环结尾的跳转，或者总是为真/假的判断），预测准确率通常在 90% 到 99% 以上。

对于这种高度可预测的分支，预测错误极少发生，因此它们对性能几乎没有副作用。程序员应该将精力集中在那些随机性强、不可预测的分支上。

书写适合用条件传送实现的代码

使用数据流的相关性代替控制流的相关性。

在 x86-64 中使用 cmov 类指令。它不会改变程序的控制流（不发生跳转），而是计算出两个可能的值，然后根据条件选择一个。

这消除了分支跳转，因此完全避免了分支预测错误处罚，并且流水线可以保持充满状态。

在 C 语言中，使用三元运算符（如 v = test ? a : b）通常比使用普通的 if-else 更容易被编译器翻译成条件传送指令。
条件传送并不总是更好。如果分支里的计算非常复杂或有副作用（例如 test ? *p : 0，即使条件不成立也会去读指针 p），那么传统的跳转分支反而更安全或更高效。

家庭作业

(´-ω-｀)