CSAPP6

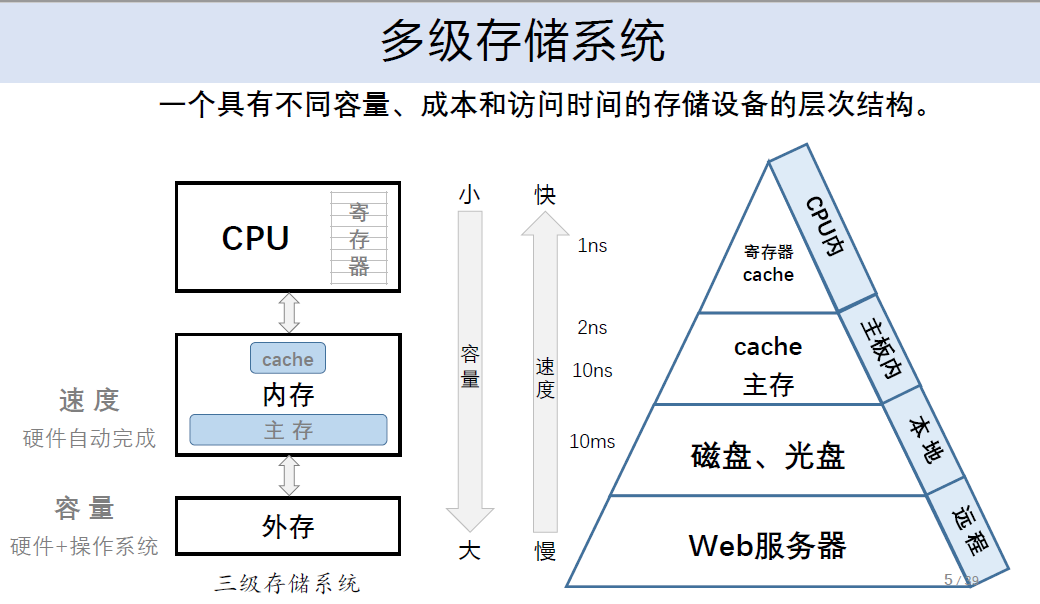
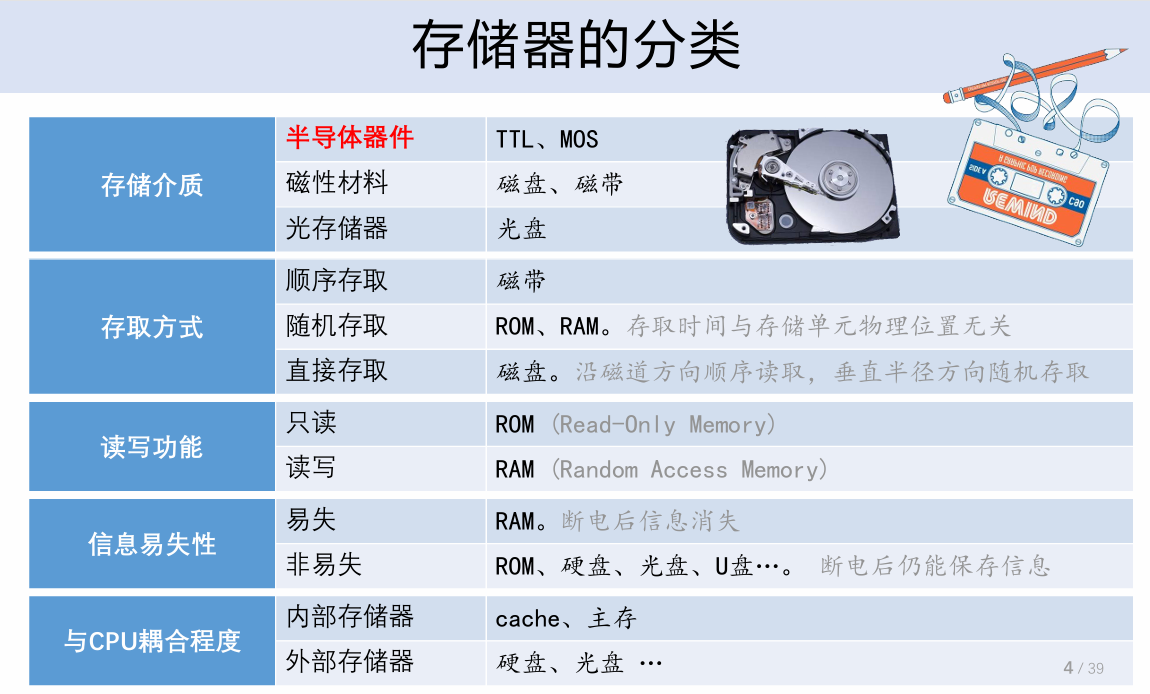
存储技术

随机访问存储器（RAM）

SRAM（静态随机存取存储器）：使用触发器存储数据，速度快但容量较小且成本高，不需要刷新。

一般用作 cache

存储元由6个晶体管组成只要有电，信息一直保存对电器干扰不敏感比DRAM更快，也更贵

DRAM（动态随机存取存储器）：使用电容器存储数据，容量大但速度较慢，需要定期刷新。

一般用作主存

特点如下：

存储元由1个电容+1个晶体管组成每隔一段时间必须刷新一次对电器干扰敏感比SRAM慢，但便宜

更具体的内部实现参考数字逻辑

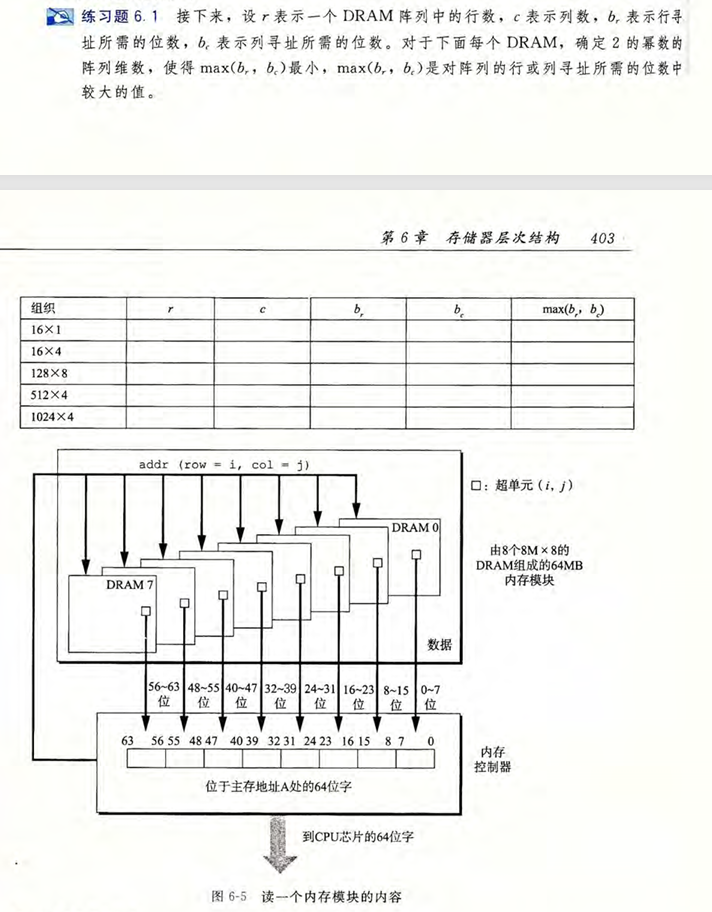
参数含义：
- 组织 ($N \times M$)：表示 DRAM 中有 $N$ 个超单元（supercells），每个超单元包含 $M$ 位（bits）。
- $r$：DRAM 阵列的行数。
- $c$：DRAM 阵列的列数。
- $b_r$：行寻址所需的位数，即 $b_r = \log_2 r$。
- $b_c$：列寻址所需的位数，即 $b_c = \log_2 c$。
约束条件：
- 总超单元数 $N = r \times c$。
- $r$ 和 $c$ 必须是 2 的幂。
- 目标是使 $\max(b_r, b_c)$ 最小。这意味着 $r$ 和 $c$ 应该尽可能接近。

组织	$r$	$c$	$b_r$	$b_c$	$\max(b_r, b_c)$
$16 \times 1$	4	4	2	2	2
$16 \times 4$	4	4	2	2	2
$128 \times 8$	16	8	4	3	4
$512 \times 4$	32	16	5	4	5
$1024 \times 4$	32	32	5	5	5

$16 \times 1$: $N=16=2^4$。$b_r+b_c=4$。取 $b_r=2, b_c=2$，则 $r=2^2=4, c=2^2=4$。$\max(2,2)=2$。
$16 \times 4$: $N=16=2^4$（超单元数依然是 16）。同上，$b_r=2, b_c=2, r=4, c=4, \max=2$。
$128 \times 8$: $N=128=2^7$。$b_r+b_c=7$。取 $b_r=4, b_c=3$，则 $r=2^4=16, c=2^3=8$。$\max(4,3)=4$。（若取 $b_r=3, b_c=4$ 结果一致）。
$512 \times 4$: $N=512=2^9$。$b_r+b_c=9$。取 $b_r=5, b_c=4$，则 $r=2^5=32, c=2^4=16$。$\max(5,4)=5$。
$1024 \times 4$: $N=1024=2^{10}$。$b_r+b_c=10$。取 $b_r=5, b_c=5$，则 $r=2^5=32, c=2^5=32$。$\max(5,5)=5$。

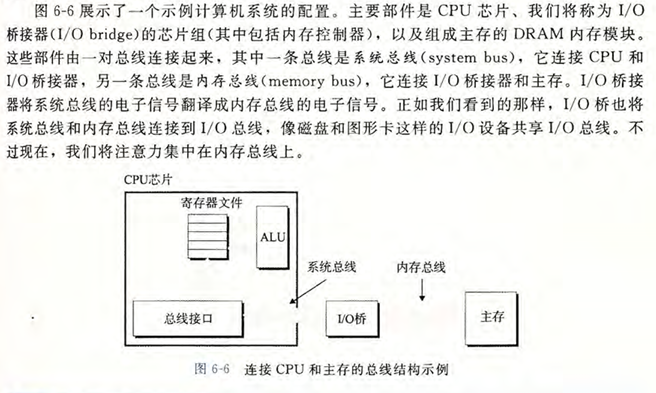
磁盘

存储

磁盘由盘片构成，盘片上有磁道，磁道上有扇区，构造如图所示

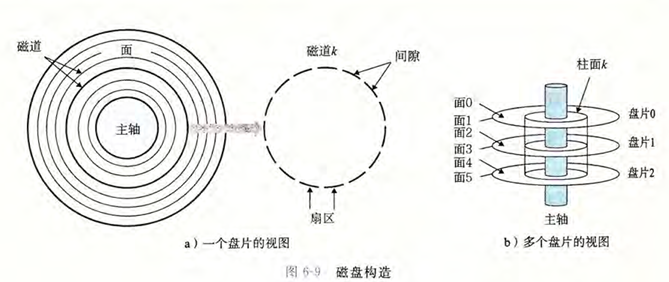
一个磁盘上可以记录的最大位数称为它的最大容量，或者简称为容量。磁盘容量是由以下技术因素决定的：

记录密度：每英寸磁道上能记录的位数，通常以每英寸位数（bpi，bits per inch）表示。
磁道密度：从盘片中心到边缘每英寸能容纳的磁道数，通常以每英寸磁道数（tpi，tracks per inch）表示。
面密度：每个盘片的记录面数。

现代大容量磁盘使用一种称为多区记录

此技术中，柱面的集合被分割为不相交的子集，称为记录区（recording zones），每个取包含连续的柱面，一个区中每个柱面中的每条磁道都有相同数量的扇区

下面公式给出了一个磁盘的容量 \[ 磁盘容量=\frac{字节数}{扇区}\times \frac{平均扇区数}{磁道} \times \frac{磁道数}{表面} \times \frac{表面数}{盘片} \times \frac{盘片数}{磁盘} \] 假设我们有一个磁盘，有 $5$ 个盘面，每个扇区 $512$ 字节，每个面 $20000$ 条磁道，每条磁道平均 $300$ 个扇区

那么这个磁盘的容量就是 $5\times 512 \times 20000 \times 2 \times 300 = 30.72GB$

需要注意的是，磁盘的容量通常以十进制计量单位表示（1GB = $10^9$ 字节），而计算机内存通常以二进制计量单位表示（1GiB = $2^{30}$ 字节）

读写

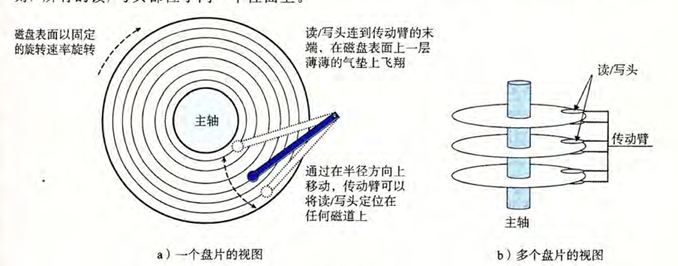
通过沿着半径轴前后移动这个传动臂，驱动器可以将读/写头定位在盘面上的任何磁道上。这样的机械运动称为寻道（seek)

当读/写头到达目标磁道后，盘片继续旋转，直到目标扇区转到读/写头下方为止。

寻道时间：找到目标磁道所需的时间$T_{avg\_seek}$

旋转时间：从目标磁道开始旋转到目标扇区到达读/写头下方所需的时间

这个步骤的性能依赖于磁盘的转速，通常以每分钟转数（RPM，revolutions per minute）表示。转速越高，平均旋转延迟越低，从而提高了读写性能。

平均旋转时间 $T_{avg\_rotation}$ 是最大旋转延迟 $T_{max\_rotation}$ 的一半：

其中最大旋转延迟 $T_{max\_rotation}$ 可以通过以下公式计算： \[ T_{max\_rotation}=\frac{1}{RPM} s \times 60 \] 传送时间：读取或写入数据所需的时间

平均传送时间 $T_{avg\_transfer}$ 可以通过以下公式计算： \[ T_{avg\_transfer}=\frac{1}{RPM}s\times 60 \times \frac{1}{平均扇区数/磁道} \] 例如，参考一个如下参数的磁盘：

转速：7200 RPM
平均扇区数/磁道：300
$T_{avg\_seek}=9ms$

那么：

$T_{max\_rotation}=\frac{1}{7200}s\times 60=8.33ms$
$T_{avg\_rotation}=\frac{8.33ms}{2}=4.17ms$
$T_{avg\_transfer}=\frac{1}{7200}s\times 60 \times \frac{1}{300}=0.0278ms$

整个访问时间就是

$T_{access}=T_{avg\_seek}+T_{avg\_rotation}+T_{avg\_transfer}=9ms+4.17ms+0.0278ms=13.1978ms$

最大访问时间就是

$T_{max\_access}=T_{avg\_seek}+T_{max\_rotation}+T_{avg\_transfer}=9ms+8.33ms+0.0278ms=17.3578ms$

SSD

SSD（固态硬盘）使用闪存技术存储数据，没有机械运动部件，因此读写速度更快，抗震性能更好，但成本较高。

SSD 读比写快

局部性

一个编写良好的计算机程序常常具有良好的局部性，也就是，它们倾向于引用邻近于其他最近引用过的数据项的数据项，或者最近引用过的数据项本身

一般而言，有良好局部性的程序比局部性差的程序运行得更快

时间局部性

被引用过一次的内存位置很可能在不远的将来再被多次引用。核心思想：“最近用过的，待会可能还要用”

代码体现：循环中的变量、累加器

空间局部性

如果一个内存位置被引用了，那么程序很可能在不远的将来引用其附近（地址相邻）的内存位置。核心思想：“附近用过的，待会可能用附近的”

代码体现：按顺序访问数组元素（步长为 1 的访问）

考虑一个简单的求和函数

int sum_array(int v[N]) {
    int i, sum = 0;

    for (i = 0; i < N; i++) {
        sum += v[i]; // <--- 这里体现了两种局部性
    }
    return sum;
}

时间局部性：极好。变量 sum 和 i 在每次循环迭代中都被访问，它们被重复使用。
空间局部性：极好。数组 v 是连续存储的，程序按照 v[0], v[1], v[2]... 的顺序访问（步长为 1），这契合了空间局部性。

但是在二位数组中

// 内存顺序：A[0][0], A[0][1], A[0][2] ... A[1][0], A[1][1]...
for (i = 0; i < M; i++) {
    for (j = 0; j < N; j++) {
        sum += A[i][j]; // 步长为1，访问的是内存中相邻的地址
    }
}

这种写法空间局部性非常好，CPU 预取（Prefetch）数据时命中率极高

// 每次循环跳转的地址很大（跳过一整行）
for (j = 0; j < N; j++) {
    for (i = 0; i < M; i++) {
        sum += A[i][j]; // 步长为 N，访问的地址在内存中是不连续的
    }
}

空间局部性极差。每次执行 i++，程序都要跳过一整行数据去取下一个元素。如果数组很大，会导致缓存频繁失效（Cache Miss），程序运行速度可能比行优先慢数倍

高速缓存 Cache

高速缓存（Cache）是一种小容量、速度极快的存储器，位于处理器和主存之间，用于临时存储频繁访问的数据和指令，以提高系统整体性能。

如图展示了存储器层次结构中缓存的一般性概念，第 $k+1$ 层的存储器被分成连续的数据对象组块，称为块

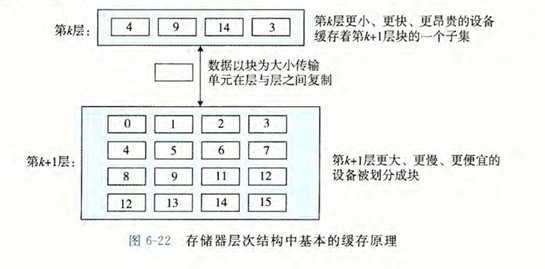
数据总是以块大小为传送单元（transfer unit)在第$k$层和第$k+1$层之间来回复制的

一般而言，层次结构中较低层(离CPU较远）的设备的访问时间较长，因此为了补偿这些较长的访问时间，倾向于使用较大的块

缓存命中

当处理器请求的数据已经存在于缓存中时，称为缓存命中（cache hit）。在这种情况下，数据可以直接从缓存中读取，访问速度非常快。

缓存不命中

当处理器请求的数据不在缓存中时，称为缓存不命中（cache miss）。此时，系统必须从较慢的主存中加载数据到缓存，然后再提供给处理器，这会导致较长的延迟。

缓存不命中分为三类

如果第 $k$ 层的缓存时空的，那么对任何数据对象访问都会不命中，空的缓存称为 冷缓存（cold cache) 或，此类不命中称为 冷不命中（cold miss) 或 强制不命中（compulsory miss)

如果缓存使用了某种映射策略（如直接映射或组相联映射），那么不同的数据块可能会映射到缓存中的同一位置，这可能导致频繁的替换和不命中，此类不命中称为 冲突不命中（conflict miss)

如果缓存容量不足以容纳所有正在使用的数据块，那么当新的数据块被加载时，可能会替换掉仍然需要的数据块，此类不命中称为 容量不命中（capacity miss)

高速缓存处理器

考虑这样一个计算机系统，其中每个存储器地址有 $m$ 位，形成一个地址空间，包含 $2^m$ 个字节的存储器

这样的机器的高速缓存被组织成一个有 $S=2^s$ 个高速缓存组的数组，每个组包含 $E$ 个高速缓存行，每个行是一个包含 $B=2^b$ 个字节的数据块

在每个数据块中，一个有效位指明该行是否包含有效数据，还有$t=m-(b+s)$ 个标记为。唯一地表示存储在这个高速缓存行中的块

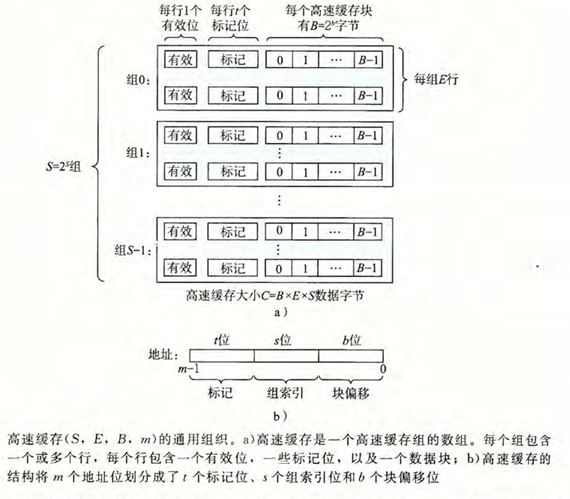
一般而言，这样的高速缓存结构可以用元组 $(S, E, B, m)$ 来表示，高速缓存的总容量 $C$ 可以通过以下公式计算：

$C = S \times E \times B \text{ 字节}$

当一条加载指令指示CPU从主存地址A中读一个字时，CPU首先检查高速缓存中是否存在包含地址A的块。如果存在（缓存命中），CPU就可以直接从高速缓存中读取数据。如果不存在（缓存不命中），则需要从主存中加载包含地址A的块到高速缓存中，然后再从高速缓存中读取数据

参数总结如下

练习 6.9

高速缓存	$m$	$C$	$B$	$E$	$S$	$t$	$s$	$b$
1.	32	1024	4	1	256	22	8	2
2.	32	1024	8	4	32	24	5	3
3.	32	1024	32	32	1	27	0	5

直接映射高速缓存

高速缓存判断一个请求是否命中，分为三步：

组选择
行匹配
字抽取

组选择

组选择使用地址的 $s$ 位组索引字段来选择高速缓存中的一个组。组索引字段位于地址的中间部分，介于标记字段和块偏移字段之间

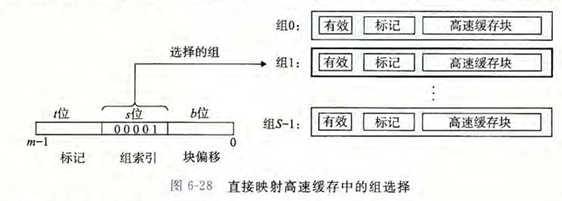
行匹配

上一步中已经选中了一个组，接下来需要在该组中的 $E$ 个行中查找与地址的标记字段匹配的行。如果找到匹配的行，并且该行的有效位被设置为 1，则表示缓存命中；否则，表示缓存不命中

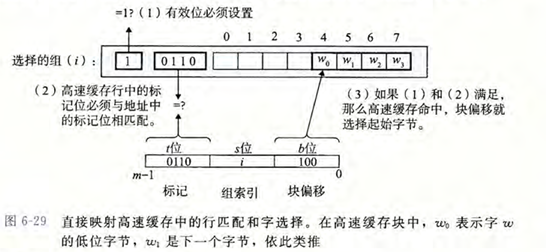
字抽取

一旦找到匹配的行，接下来需要从该行的数据块中提取所需的字。块偏移字段用于确定数据块中的具体字位置

行替换

当发生缓存不命中时，需要将主存中的数据块加载到缓存中。如果所选组中的所有行都已被占用（即有效位均为 1），则需要选择一个行进行替换。

一般而言，如果组中都是有效高速缓存行了，那么必须要驱逐出一个现存的行。对于直接映射高速缓存来说，每个组只包有一行，替换策略非常简单：用新取出的行替换当前的行。

当程序访问大小为 2 的幂的数组时，直接映射高速缓存中通常会发生冲突不命中。例如，考虑一个计算两个向量点积的函数

float dot_product(float x[8], float y[8]) {
    float sum = 0.0;
    int i;

    for (i = 0; i < 8; i++) {
        sum += x[i] * y[i];
    }
    return sum;
}

这个函数的空间局部性很好，因为它按顺序访问数组 x 和 y 的元素。然而，如果高速缓存的大小为 16 字节，并且每个块包含 4 字节（即一个浮点数），那么数组 x 和 y 的元素将映射到相同的缓存组中，导致频繁的冲突不命中。

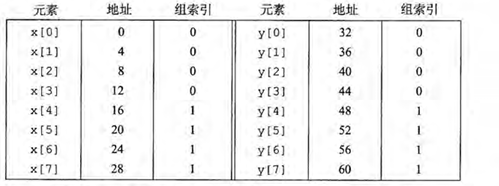
在运行时，访问 x[0] 会将其加载到缓存中。接下来，访问 y[0] 会导致冲突不命中，因为它映射到相同的缓存组，迫使 x[0] 被替换出缓存。这个过程会在每次访问 x[i] 和 y[i] 时重复发生，导致大量的缓存不命中，从而显著降低程序的性能

但我们可以通过强制增大缓存的块大小来缓解这个问题。例如，如果我们将数组大小增加到 12 ）

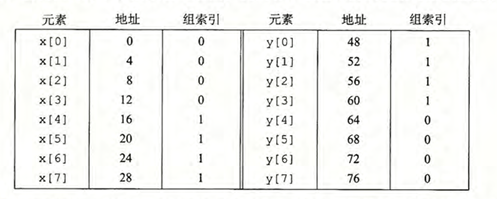
$x$ 和 $y$ 映射到不同组，从而避免了冲突不命中，提高了缓存的命中率和程序的性能。

组相连高速缓存

直接映射高速缓存中冲突不命中造成的问题源于每个组只有一行

组相连高速缓存通过允许每个组包含多个行来缓解这个问题，从而减少冲突不命中的发生

组选择

和直接映射缓存类似，组相连缓存使用地址的 $s$ 位组索引字段来选择高速缓存中的一个组

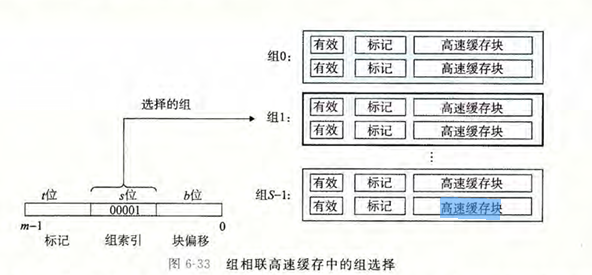
行匹配和字选择

比直接映射缓存多了一步：在选中的组中查找与地址的标记字段匹配的行。如果找到匹配的行，并且该行的有效位被设置为 1，则表示缓存命中；否则，表示缓存不命中

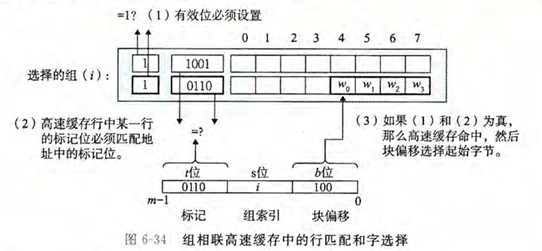
行替换

当发生缓存不命中时，需要将主存中的数据块加载到缓存中。如果所选组中的所有行都已被占用（即有效位均为 1），则需要选择一个行进行替换。组相连缓存通常使用更复杂的替换策略

最近最少使用（LRU，Least Recently Used）策略，即替换掉在最近一段时间内最少被访问的行

最不常使用（LFU，Least Frequently Used）策略，即替换掉访问频率最低的行

全相连高速缓存

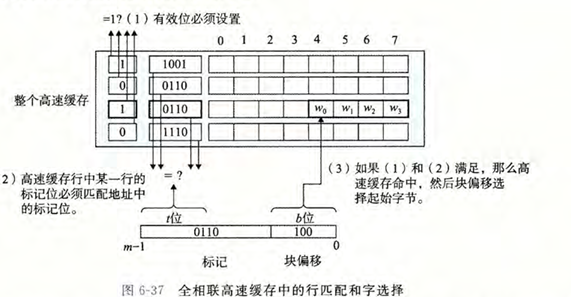
全相连高速缓存是组相连缓存的一个极端情况，其中整个缓存被视为一个单一的组，包含所有的行

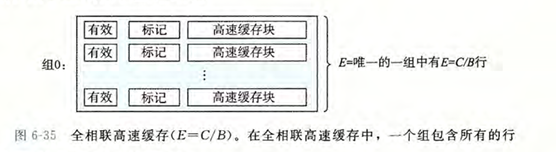
在全相连缓存中，任何主存块都可以存储在缓存的任何行中，这种灵活性极大地减少了冲突不命中的可能性

组选择

全相连缓存没有组索引字段，因为整个缓存被视为一个单一的组

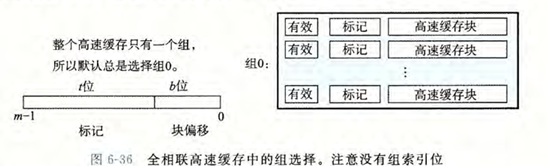
行匹配和字选择

在全相连缓存中，行匹配涉及检查缓存中的所有行，以查找与地址的标记字段匹配的行。如果找到匹配的行，并且该行的有效位被设置为 1，则表示缓存命中；否则，表示缓存不命中

有关写的问题

假设我们要写一个已经缓存了的字$w$，写命中，writehit)

直写法（write-through）

在这种方法中，每当 CPU 写入缓存中的数据时，数据也会立即写入主存。这确保了缓存和主存之间的数据一致性，但可能导致较高的写延迟，因为每次写操作都需要访问较慢的主存。

写回法（write-back）

在这种方法中，当 CPU 写入缓存中的数据时，数据仅更新缓存，而不立即写入主存。只有当缓存行被替换时，才将修改过的数据写回主存。这种方法减少了对主存的写操作，提高了性能，但需要额外的机制来跟踪哪些缓存行已被修改（通常使用一个称为“脏位”的标志位）。

写不命中

当 CPU 尝试写入一个不在缓存中的字时，发生写不命中（write miss）。处理写不命中的方法有两种主要策略：

写分配（write-allocate）

在这种策略中，当发生写不命中时，系统会先将包含目标字的块从主存加载到缓存中，然后再执行写操作。这种方法适用于局部性较好的情况，因为加载整个块可能会使后续的写操作更快。

非写分配（no-write-allocate）

在这种策略中，当发生写不命中时，系统直接将数据写入主存，而不将块加载到缓存中。这种方法适用于局部性较差的情况，因为加载整个块可能不会带来性能提升。

编写高速缓存友好的代码

让最常见的情况运行的快

程序的大部分执行时间通常花在少数核心循环上。应该把优化的重心放在这些“热点”区域（通常是嵌套循环的最内层）。

减少内层循环的计算量，确保内层循环的数据访问具有良好的局部性。

尽量减少每个循环内部的缓存不命中量

利用空间局部性（步长为 1 的访问）和时间局部性（重复使用缓存中的数据）

代码示例与对比

A. 空间局部性：步长 (Stride) 的重要性

假设我们有一个二维数组 a[M][N]，在 C 语言中它是按行优先（Row-major）存储的。

推荐：高速缓存友好型（步长为 1）

// 扫描顺序：a[0][0], a[0][1], a[0][2]...
// 每一个缓存行（Cache Line）读入后，后续的几个元素都会命中
for (i = 0; i < M; i++) {
    for (j = 0; j < N; j++) {
        sum += a[i][j]; // 内层循环沿行移动
    }
}

为什么快？：当 CPU 加载 a[0][0] 时，它会顺便把后面的一整块数据（例如 64 字节，包含多个 int）都加载到缓存行中。访问 a[0][1] 时，数据已经在缓存里了。

不推荐：高速缓存不友好型（步长为 N）

// 扫描顺序：a[0][0], a[1][0], a[2][0]...
// 每次移动都会跳过一整行，极易导致缓存不命中
for (j = 0; j < N; j++) {
    for (i = 0; i < M; i++) {
        sum += a[i][j]; // 内层循环沿列移动
    }
}

为什么慢？：如果数组很大，每次 i++ 访问的地址距离上一个地址非常远。上一次加载的缓存行还没被用到就可能被替换掉，导致频繁的 Cache Miss。

B. 时间局部性：变量复用

示例：局部变量的使用

void sum_vec(int v[N], int *res) {
    int i;
    int temp = 0; // 使用局部变量（通常在寄存器或一级缓存中）

    for (i = 0; i < N; i++) {
        temp += v[i]; 
    }
    *res = temp; // 最后才写回主存地址
}

分析：这里 temp 展现了极好的时间局部性。在整个循环中，temp 被反复引用。相比于每次循环都直接修改指针指向的内容（*res += v[i]），使用局部变量能减少对内存（或高层缓存）的写操作，让“最常见的情况”运行得更快。

家庭作业

6.22

磁道数量与 $(1-x)r$ 成正比，磁道位数和 $xr$ 成正比，设为

总容量位数为 $C$，则有：$C(x)=K(x-x^2)$，最大时$x=0.5$。

6.23

平均寻道时间 $T_1=4ms$

最大旋转延迟 $T_m=\frac{60}{15000}=4ms$

平均旋转延迟 $T_2=2ms$

平均传输时间 $T_3=\frac{1}{15000}\times \frac{1}{800}\times 10^3=0.005ms$

总时间 $T=T_1+T_2+T_3=6.005ms$

6.24

平均寻道时间 $T_1=4ms$

最大旋转延迟 $T_m=\frac{60}{15000}=4ms$

平均旋转延迟 $T_2=2ms$

$2MB$ 的文件， $2MB=2^{21}$字节，扇区大小 $512$字节，块数为 $\frac{2^{21}}{2^9}=2^{12}=4096$块

最好情况时，一个接一个，读取时间 $T_3=\frac{4096}{1000}\times T_m==16.384ms$

总时间 $22.384ms$

随机情况时，读取每个块都要先寻道和等待旋转，读取

对于一个块，寻找时间为 $T_1+T_2+\frac{1}{1000} \times T_m = 6.004ms$

总时间 $T=4096\times 6.004ms=24586.384ms$

6.25

高速缓存	m	C	B	E	S	t	s	b
1.	$32$	$1024$	$4=2^2$	$4=2^2$	$64 $	$24$	$6$	$2$
2.	$32$	$1024$	$4=2^2$	$256=2^8$	$1$	$30$	$0$	$2$
3.	$32$	$1024$	$8=2^3$	$1$	$128$	$22$	$7$	$3$
4.	$32$	$1024$	$8=2^3$	$128=2^7$	$1$	$29$	$0$	$3$
5.	$32$	$1024$	$32=2^5$	$1$	$32$	$22$	$5$	$5$
6.	$32$	$1024$	$32=2^5$	$4=2^2$	$8$	$24$	32$	$5$

6.26

高速缓存	m	C	B	E	S	t	s	b
1.	$32$	$2048$	$8=2^3$	$1=2^0$	$2^8=256$	$21$	$8$	$3$
2.	$32$	$2048$	$4=2^2$	$4$	$128=2^7$	$23$	$7$	$2$
3.	$32$	$1024$	$2=2^1$	$8=2^3 $	$64=2^6 $	$25$	$6$	$1$
4.	$32$	$1024$	$2^5=32$	$2=2^1$	$16=2^4$	$23$	$4$	$5$

6.27

0b0100 0101 001 00 = 0x08A4

0b0100 0101 001 01 = 0x08A5

0b0100 0101 001 10 = 0x08A6

0b0100 0101 001 11 = 0x08A6

0b0011 1000 001 00 = 0x0704

0b0011 1000 001 01 = 0x0705

0b0011 1000 001 10 = 0x0706

0b0011 1000 001 11 = 0x0707

0b1001 0001 110 00 = 0x1238

0b1001 0001 110 01 = 0x1239

0b1001 0001 110 10 = 0x123A

0b1001 0001 110 11 = 0x123B

6.28

无

0b1100 0111 100 00 = 0x18F0

0b1100 0111 100 01 = 0x18F1

0b1100 0111 100 10 = 0x18F2

0b1100 0111 100 11 = 0x18F3

0b0000 0101 100 00 = 0x00B0

0b0000 0101 100 01 = 0x00B1

0b0000 0101 100 10 = 0x00B2

0b0000 0101 100 11 = 0x00B3

0b0111 0001 101 00 = 0x0E34

0b0111 0001 101 01 = 0x0E35

0b0111 0001 101 10 = 0x0E36

0b0111 0001 101 11 = 0x0E37

0b1101 1110 111 00 = 0x1BDC

0b1101 1110 111 01 = 0x1BDD

0b1101 1110 111 10 = 0x1BDE

0b1101 1110 111 11 = 0x1BDF

6.29

12	11	10	9	8	7	6	5	4	3	2	1	0
?	CT	CT	CT	CT	CT	CT	CT	CT	CI	CI	CO	CO

操作	地址	命中	读出的值
读	0x834	未命中	-
写	0x836	命中	未知
读	0xFFD	命中	C0

6.30

E=4，B=4，S=8，C=128字节

12	11	10	9	8	7	6	5	4	3	2	1	0
CT	CT	CT	CT	CT	CT	CT	CT	CI	CI	CI	CO	CO

6.31

0011 1000 110 10

CO：0x2

CI：0x6

CT：0x38

命中

6.32

1011 0111 010 00

CO：0x0

CI：0x2

CT：0xB7

未命中

6.33

0b 1011 1100 010 00 = 0x1788

0b 1011 1100 010 01 = 0x1789

0b 1011 1100 010 10 = 0x178A

0b 1011 1100 010 11 = 0x178B

0b 1011 0110 010 00 = 0x16C8

0b 1011 0110 010 01 = 0x16C9

0b 1011 0110 010 10 = 0x16CA

0b 1011 0110 010 11 = 0x16CB

6.34

直接映射,E=1，B=16，C=32，S=2

m表示不命中，h表示命中

int4字节，一次可取数组一行

dst

m	m	m	m
m	m	m	m
m	m	m	m
m	m	m	m

src

m	m	h	m
m	h	m	h
m	m	h	m
m	h	m	h

6.35

直接映射，E=1，B=16，C=128，S=8

dst

m	m	m	m
m	m	m	m
m	m	m	m
m	m	m	m

src

m	h	h	h
m	h	h	h
m	h	h	h
m	h	h	h

6.36

C=512，直接映射，E=1，B=16，S=32

块 16 字节，一个块读取 4 个整型

x[2][128]，一行512字节

x[0][0] 地址 0x0000-0x0004

x[1][0] 地址 0x0200-0x0204

x[0][0] 映射到组：$(0 / 16) \bmod 32 = \mathbf{0}$

x[1][0] 映射到组：$(512 / 16) \bmod 32 = 32 \bmod 32 = \mathbf{0}$

两个元素映射到同一个组，一定会冲突

不命中率 100%

C=1024，直接映射，E=1，B=16，S=64

x[0][0] 映射到组：$(0 / 16) \bmod 64 = 0$

x[1][0] 映射到组：$(512 / 16) \bmod 64 = 32$

一个块读取 4 个整型

访问 4 个有 1 个不命中

128/4 = 32，正好到第 32 组，后面不会发生驱逐

不命中率 25%

C=512，E=2，B=16，S=16

x[0][0] 映射到组：$(0 / 16) \bmod 16 = 0$

x[1][0] 映射到组：$(512 / 16) \bmod 16 = 32 \bmod 16 = 0$

但是由于是 2 路组相联，可以同时存放两个块

访问 4 个有 1 个不命中

不命中率 25%

更大的高速缓存大小会让S更大，但是会发生冷不命中，只要这两块能同时塞进组里，再大的缓存也不会减少冷不命中的次数

更大的块大小每次取的数据更多，减少了不命中的次数

6.37

C=4KB=4096字节

B=16字节，S=256组

E=1，直接映射

当 N=64 时，

sumA

一次能取出 4 个数据，不命中率 25%

sumB

正好 64 mod 16 = 0，不命中率 100%

sumC

一次取一个方块，每个方块每行的第二个是命中的，不命中率 50%

当 N=60 时，

sumA

同理，不命中率 25%

sumB

两行之间的地址差为

60×4=24060×4=240字节

在 Cache 中相隔 240/16=15240/16=15 个块

步长不再导致 Cache 组冲突，加载的块能长时间保存在 Cache 中

不命中率 25%

sumC

同理，不命中率 25%

6.38

C=2048

直接映射，E=1

B=32，S=64

结构体4个整型占 16 字节

每次预取占 2 个结构体

写总数 $16*16*4=1028$

高速缓存中不命中 1/8 ，共 128 次

不命中率 12.5%

6.39

变为列优先了，由于每行 16*16=256 字节，块大小 32 字节

$256/32 mod 64= 8$，每 $8$ 个会冲突一次

不命中率提高到 25%

写总数不变，1028

不命中 256

不命中率 25%

6.40

先循环一个变量，其他不改，第二次正好冲突，重新读，提高一倍

写总数不变

不命中 256

不命中率 25%

6.41

C=64KB=65536字节

总计480 × 640 = 307,200次写缓存大小65,536字节，能存16,384行

不命中率是25%

因此写不命中次数是72800次

6.42

25%

6.43

100%

组织	\(r\)	\(c\)	\(b_r\)	\(b_c\)	\(\max(b_r, b_c)\)
\(16 \times 1\)	4	4	2	2	2
\(16 \times 4\)	4	4	2	2	2
\(128 \times 8\)	16	8	4	3	4
\(512 \times 4\)	32	16	5	4	5
\(1024 \times 4\)	32	32	5	5	5

高速缓存	m	C	B	E	S	t	s	b
1.	\(32\)	\(1024\)	\(4=2^2\)	\(4=2^2\)	$64 $	\(24\)	\(6\)	\(2\)
2.	\(32\)	\(1024\)	\(4=2^2\)	\(256=2^8\)	\(1\)	\(30\)	\(0\)	\(2\)
3.	\(32\)	\(1024\)	\(8=2^3\)	\(1\)	\(128\)	\(22\)	\(7\)	\(3\)
4.	\(32\)	\(1024\)	\(8=2^3\)	\(128=2^7\)	\(1\)	\(29\)	\(0\)	\(3\)
5.	\(32\)	\(1024\)	\(32=2^5\)	\(1\)	\(32\)	\(22\)	\(5\)	\(5\)
6.	\(32\)	\(1024\)	\(32=2^5\)	\(4=2^2\)	\(8\)	\(24\)	32$	\(5\)

高速缓存	m	C	B	E	S	t	s	b
1.	\(32\)	\(2048\)	\(8=2^3\)	\(1=2^0\)	\(2^8=256\)	\(21\)	\(8\)	\(3\)
2.	\(32\)	\(2048\)	\(4=2^2\)	\(4\)	\(128=2^7\)	\(23\)	\(7\)	\(2\)
3.	\(32\)	\(1024\)	\(2=2^1\)	$8=2^3 $	$64=2^6 $	\(25\)	\(6\)	\(1\)
4.	\(32\)	\(1024\)	\(2^5=32\)	\(2=2^1\)	\(16=2^4\)	\(23\)	\(4\)	\(5\)

高速缓存	\(m\)	\(C\)	\(B\)	\(E\)	\(S\)	\(t\)	\(s\)	\(b\)
1.	32	1024	4	1	256	22	8	2
2.	32	1024	8	4	32	24	5	3
3.	32	1024	32	32	1	27	0	5

(´-ω-｀)

CSAPP6

存储技术

随机访问存储器（RAM）

磁盘

存储

读写

SSD

局部性

时间局部性

空间局部性

高速缓存 Cache

缓存命中

缓存不命中

高速缓存处理器

直接映射高速缓存

组选择

行匹配

字抽取

行替换

组相连高速缓存

组选择

行匹配和字选择

行替换

全相连高速缓存

组选择

行匹配和字选择

有关写的问题

直写法（write-through）

写回法（write-back）

写不命中

写分配（write-allocate）

非写分配（no-write-allocate）

编写高速缓存友好的代码

让最常见的情况运行的快

尽量减少每个循环内部的缓存不命中量

代码示例与对比

A. 空间局部性：步长 (Stride) 的重要性

B. 时间局部性：变量复用

家庭作业

6.22

6.23

6.24

6.25

6.26

6.27

6.28

6.29

6.30

6.31

6.32

6.33

6.34

6.35

6.36

6.37

6.38

6.39

6.40

6.41

6.42

6.43