集合与图论学习笔记06

定义

定义 6.1 子图、生成子图、边导出子图、导出子图

设 \(G=(V,E)\) 是一个无向图，\(G'=(V',E')\) 也是一个无向图。如果 \(V' \subseteq V\) 且 \(E' \subseteq E\)，则称 \(G'\) 是 \(G\) 的一个子图

若 \(G'\) 是 \(G\) 的一个子图，且 \(V' = V\)，则称 \(G'\) 是 \(G\) 的一个生成子图

若对于 \(E' \subseteq E\) ，以 \(E'\) 为边集，所关联的所有顶点为顶点集 \(V'\)，，图\(G'=(V',E')\) 是 \(G\) 的一个边导出子图，记为 \(G(E)\)

设 \(V'\subseteq V\)，以 \(V'\) 为顶点集，\(E' \subseteq E\) 且 \(E'\) 中的每一条边都连接 \(V'\) 中的顶点，则图 \(G'=(V',E')\) 是 \(G\) 的一个导出子图，记为 \(G(V)\)

显然，完全图的导出子图还是完全图

定理 6.1.1

每个 \(n\) 个顶点的简单图同构于 \(K_n\) 的一个子图

证明： 点击查看证明

证明：

设 \(G=(V,E)\) 是一个有 \(n\) 个顶点的简单图，\(V=\{v_1,v_2,\ldots,v_n\}\)

构造映射 \(f: V \to V(K_n)\)，使得 \(f(v_i)=u_i\)，其中 \(u_i\) 是 \(K_n\) 的顶点。由于 \(G\) 是简单图，任意两顶点间最多有一条边，因此对于任意边 \(v_iv_j \in E\)，在 \(K_n\) 中对应的边 \(u_iu_j\) 也存在

反之，如果 \(u_iu_j\) 在 \(K_n\) 中存在，则对应的边 \(v_iv_j\) 也在 \(G\) 中存在

因此，映射 \(f\) 保持了顶点间的连接关系，即 \(G\) 同构于 \(K_n\) 的一个子图

定义 6.2 二分图

图 \(G=(V,E)\) 如果存在 \(V\) 的一个划分 \(V=V_1 \cup V_2\)，使得 \(G\) 的每一条边都连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点，这样的图称为二分图（偶图）

如果二分图 \(G=(V_1 \cup V_2,E)\) 中，\(|V_1|=|V_2|=n\)，且 \(G\) 中的每一条可能的边都存在，则称 \(G\) 为完全二分图，记为 \(K_{n,n}\)

定理 6.2.1

一个图是二分图的充分必要条件是它不包含奇回路

证明： 点击查看证明

证明：(必要性)

设 \(G=(V,E)\) 是一个二分图，\(V=V_1 \cup V_2\) 是 \(V\) 的一个划分

假设 \(G\) 中存在一个奇数长度的回路 \(C\)，则 \(C\) 必须交替经过 \(V_1\) 和 \(V_2\) 的顶点

由于回路的长度为奇数，起点和终点必须在同一集合中，这与二分图的定义矛盾

因此，二分图中不可能存在奇数长度的回路。

(充分性) 设 \(G=(V,E)\) 是一个不包含奇数长度回路的图

选择任意顶点 \(v_0 \in V\)，令 \(V_1\) 为 \(v_0\) 到所有奇数长度路径的终点集合，\(V_2\) 为 \(v_0\) 到所有偶数长度路径的终点集合

下面证明 \(V=V_1 \cup V_2\) 是 \(V\) 的一个划分

\(G\) 是连通的，所以 \(V_1 \cup V_2 = V\)，且 \(V_1 \cap V_2 = \emptyset\)，否则存在一个顶点 \(v\) 同时在 \(V_1\) 和 \(V_2\) 中，这意味着存在一条从 \(v_0\) 到 \(v\) 的奇数长度路径和一条偶数长度路径，这将形成一个奇数长度回路，与假设矛盾

下面证明\(G\) 的每一条边都连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点

假设存在一条边 \(uv \in E\)，其中 \(u,v \in V_1\)，则存在从 \(v_0\) 到 \(u\) 的奇路和从 \(v_0\) 到 \(v\) 的奇路，将这两条路径与边 \(uv\) 连接起来，将形成一个奇数长度回路，这与假设矛盾

同理，如果 \(u,v \in V_2\)，也会导致矛盾

因此，\(G\) 的每一条边都连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点，\(G\) 是一个二分图

定理 6.2.2

设 \(G=(V_1 \cup V_2,E)\) 是一个二分图，则 \(|E| \leq |V_1| \cdot |V_2|\)

证明： 点击查看证明

证明：

设 \(|V_1|=m\)，\(|V_2|=n\)，则 \(G\) 中的每一条边都连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点

因此，\(G\) 中的边数 \(|E|\) 不超过 \(V_1\) 中的每个顶点与 \(V_2\) 中的每个顶点之间可能的连接数，即 \(m \cdot n\)

即 \(|E| \leq |V_1| \cdot |V_2|\)

定理 6.2.3

二分图的每个生成子图仍然是二分图

证明： 点击查看证明

证明：

设 \(G=(V_1 \cup V_2,E)\) 是一个二分图，\(G'=(V_1 \cup V_2,E')\) 是 \(G\) 的一个生成子图，其中 \(E' \subseteq E\)

由于 \(G\) 是二分图，\(G\) 的每一条边都连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点

因此，\(G'\) 中的每一条边也连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点

所以，\(G'\) 仍然是一个二分图

定义 6.3 欧拉图

设 \(G=(V,E)\) 是一个无向图，如果 \(G\) 中存在一条经过每一条边且仅经过一次的闭迹（闭链）（回路），则称 \(G\) 为欧拉图，这样的闭迹称为欧拉闭链（欧拉回路）（欧拉链）

如果存在一条过每一条边且仅经过一次的开迹（开链），则称 \(G\) 为半欧拉图，这样的开迹称为欧拉开链

显然，欧拉图除了孤立点外是连通的，而孤立点的有无不影响图的性质，所以不妨设欧拉图是连通的

若连通有向图存在一条经过每一条有向边且仅经过一次的闭链，则称该有向图为有向欧拉图

定理 6.3.1

设 \(G=(V,E)\) 是一个连通图，则 \(G\) 是欧拉图的充分必要条件是 \(G\) 的每个顶点的度都是偶数

证明： 点击查看证明

证明：(必要性)

设 \(G=(V,E)\) 是一个欧拉图，存在一条经过每一条边且仅经过一次的闭迹 \(C\)

在闭迹 \(C\) 中，每次经过一个顶点 \(v\) 时，都会使用两条边：一条进入 \(v\)，另一条离开 \(v\)。因此，顶点 \(v\) 的度数必须是偶数

(充分性)

设 \(G=(V,E)\) 是一个连通图，且每个顶点的度都是偶数

可以通过以下步骤构造一条经过每一条边且仅经过一次的闭迹：

1. 从任意顶点 \(v_0\) 出发，沿着未经过的边行走，直到回到起点 \(v_0\)，形成一个闭迹 \(C_1\)
2. 如果 \(C_1\) 已经经过了所有的边，则完成。如果还有未经过的边，选择一个在 \(C_1\) 上的顶点 \(v_1\)，从 \(v_1\) 出发，沿着未经过的边行走，直到回到 \(v_1\)，形成另一个闭迹 \(C_2\)，由于顶点的度是偶数，\(G\) 又是连通的，所以这样的 \(v_1\) 总能找到
3. 将闭迹 \(C_2\) 插入到闭迹 \(C_1\) 中，形成一个更长的闭迹
4. 重复步骤 2 和 3，直到所有的边都被经过

由于每个顶点的度都是偶数，以上过程总能完成，最终形成一条经过每一条边且仅经过一次的闭迹，因此 \(G\) 是欧拉图

定理 6.3.2

\(G\) 是一个连通图，则 \(G\) 是半欧拉图的充分必要条件是 \(G\) 恰有两个奇度顶点

证明： 点击查看证明

证明：(必要性)

设 \(G=(V,E)\) 是一个半欧拉图，存在一条经过每一条边且仅经过一次的开迹 \(C\)，其起点为 \(u\)，终点为 \(v\)

在开迹 \(C\) 中，除了起点 \(u\) 和终点 \(v\) 外，每次经过一个顶点 \(w\) 时，都会使用两条边：一条进入 \(w\)，另一条离开 \(w\)。因此，顶点 \(w\) 的度数必须是偶数

对于起点 \(u\)，它有一条边离开但没有边进入，因此其度数是奇数。同理，终点 \(v\) 也有一条边进入但没有边离开，因此其度数也是奇数

(充分性)

设 \(G=(V,E)\) 是一个连通图，且恰有两个奇度顶点 \(u\) 和 \(v\)

可以通过以下步骤构造一条经过每一条边且仅经过一次的开迹：

1. 从奇度顶点 \(u\) 出发，沿着未经过的边行走，直到到达奇度顶点 \(v\)，形成一条开迹 \(C_1\)
2. 如果 \(C_1\) 已经经过了所有的边，则完成。如果还有未经过的边，选择一个在 \(C_1\) 上的顶点 \(w\)，从 \(w\) 出发，沿着未经过的边行走，直到回到 \(w\)，形成一个闭迹 \(C_2\)，由于顶点的度是偶数，\(G\) 又是连通的，所以这样的 \(w\) 总能找到
3. 将闭迹 \(C_2\) 插入到开迹 \(C_1\) 中，形成一个更长的开迹
4. 重复步骤 2 和 3，直到所有的边都被经过

由于每个顶点的度都是偶数，除了 \(u\) 和 \(v\)，以上过程总能完成，最终形成一条经过每一条边且仅经过一次的开迹，因此 \(G\) 是半欧拉图

定理 6.3.3

设 \(G=(V,E)\) 是一个连通图，则 \(G\) 是欧拉图当且仅当 \(G\) 是若干条边不相重的回路的并

证明： 点击查看证明

证明：

(必要性)

设 \(G=(V,E)\) 是一个欧拉图，存在一条经过每一条边且仅经过一次的闭迹 \(C\)

可以将闭迹 \(C\) 分解为若干条边不相重的回路的并

具体地，可以从闭迹 \(C\) 中选择一个顶点 \(v\)，沿着闭迹 \(C\) 行走，直到回到顶点 \(v\)，形成一个回路 \(C_1\)。然后，从闭迹 \(C\) 中去掉回路 \(C_1\) 的边，继续选择一个顶点，重复上述过程，直到所有的边都被包含在若干条回路中

(充分性)

\(G\) 是若干条边不相重的回路的并，设这些回路为 \(C_1, C_2, \ldots, C_k\)

由于这些回路的边不相重，\(G\) 是连通的，因此可以通过以下步骤构造一条经过每一条边且仅经过一次的闭迹：

1. 从任意回路 \(C_1\) 出发，沿着回路行走，直到回到起点，形成一个闭迹 \(C\)
2. 如果 \(C\) 已经经过了所有的边，则完成。如果还有未经过的边，选择一个在 \(C\) 上的顶点 \(v\)，从 \(v\) 出发，沿着未经过的回路行走，直到回到 \(v\)，形成另一个回路 \(C'\)
3. 将回路 \(C'\) 插入到闭迹 \(C\) 中，形成一个更长的闭迹
4. 重复步骤 2 和 3，直到所有的边都被经过

因此，\(G\) 是欧拉图

定理 6.3.4

\(G\) 是连通有向图，则 \(G\) 是有向欧拉图的充分必要条件是每个顶点的入度等于出度

证明： 点击查看证明

证明：

(必要性)

设 \(G=(V,E)\) 是一个有向欧拉图，存在一条经过每一条有向边且仅经过一次的闭迹 \(C\)

在闭迹 \(C\) 中，每次经过一个顶点 \(v\) 时，都会使用一条有向边进入 \(v\)，另一条有向边离开 \(v\)。因此，顶点 \(v\) 的入度必须等于出度

(充分性)

若设 \(G=(V,E)\) 是一个连通有向图，且每个顶点的入度等于出度

可以通过以下步骤构造一条经过每一条有向边且仅经过一次的闭迹：

1. 从任意顶点 \(v_0\) 出发，沿着未经过的有向边行走，直到回到起点 \(v_0\)，形成一个闭迹 \(C_1\)
2. 若果 \(C_1\) 已经经过了所有的有向边，则完成。如果还有未经过的有向边，选择一个在 \(C_1\) 上的顶点 \(v_1\)，从 \(v_1\) 出发，沿着未经过的有向边行走，直到回到 \(v_1\)，形成另一个闭迹 \(C_2\)，由于每个顶点的入度等于出度，\(G\) 又是连通的，所以这样的 \(v_1\) 总能找到
3. 将闭迹 \(C_2\) 插入到闭迹 \(C_1\) 中，形成一个更长的闭迹
4. 重复步骤 2 和 3，直到所有的有向边都被经过

因此，\(G\) 是有向欧拉图

定理 6.3.5

\(G\) 是连通有向图，则 \(G\) 是有向半欧拉图的充分必要条件是恰有一个顶点的出度比入度大 1，恰有一个顶点的入度比出度大 1，且这两个顶点都是奇点，其余顶点的入度等于出度

证明： 点击查看证明

证明：(必要性)

设 \(G=(V,E)\) 是一个有向半欧拉图，存在一条经过每一条有向边且仅经过一次的开迹 \(C\)，其起点为 \(u\)，终点为 \(v\)

在开迹 \(C\) 中，除了起点 \(u\) 和终点 \(v\) 外，每次经过一个顶点 \(w\) 时，都会使用一条有向边进入 \(w\)，另一条有向边离开 \(w\)。因此，顶点 \(w\) 的入度必须等于出度

对于起点 \(u\)，它有一条有向边离开但没有有向边进入，因此其出度比入度大 1。同理，终点 \(v\) 也有一条有向边进入但没有有向边离开，因此其入度比出度大 1

(充分性)

若设 \(G=(V,E)\) 是一个连通有向图，且恰有一个顶点 \(u\) 的出度比入度大 1，恰有一个顶点 \(v\) 的入度比出度大 1，且这两个顶点都是奇点，其余顶点的入度等于出度

可以通过以下步骤构造一条经过每一条有向边且仅经过一次的开迹：

1. 从奇度顶点 \(u\) 出发，沿着未经过的有向边行走，直到到达奇度顶点 \(v\)，形成一条开迹 \(C_1\)
2. 若果 \(C_1\) 已经经过了所有的有向边，则完成。如果还有未经过的有向边，选择一个在 \(C_1\) 上的顶点 \(w\)，从 \(w\) 出发，沿着未经过的有向边行走，直到回到 \(w\)，形成一个闭迹 \(C_2\)，由于每个顶点的入度等于出度，\(G\) 又是连通的，所以这样的 \(w\) 总能找到
3. 将闭迹 \(C_2\) 插入到开迹 \(C_1\) 中，形成一个更长的开迹
4. 重复步骤 2 和 3，直到所有的有向边都被经过

因此，\(G\) 是有向半欧拉图

欧拉图和一笔画问题密切相关

一笔画问题是指在不重复经过任何边的情况下，能否从一个顶点出发，经过图中的所有边并回到起点。根据欧拉图的定义，如果一个图是欧拉图，那么它就可以通过一笔画完成

定理 6.3.6

若一个图中奇顶点的个数为 \(2k\) 个，则该图是 \(k\) 笔画的，即可以用 \(k\) 条不重复经过任何边的路径覆盖图中的所有边

证明： 点击查看证明

证明：

设 \(G=(V,E)\) 是一个图，奇顶点的个数为 \(2k\) 个

将这 \(2k\) 个奇顶点两两配对，连接每一对奇顶点之间添加一条边，得到一个新图 \(G'=(V,E')\)，其中 \(E' = E \cup \{(u_i,v_i) | i=1,2,\ldots,k\}\)，\(u_i\) 和 \(v_i\) 是配对的奇顶点

在新图 \(G'\) 中，每个顶点的度数都是偶数，因此根据定理 6.3.1，\(G'\) 是一个欧拉图

存在一条经过每一条边且仅经过一次的闭迹 \(C\) 在 \(G'\) 中

由于 \(C\) 包含了新添加的 \(k\) 条边，我们可以将闭迹 \(C\) 分解为 \(k\) 条路径，每条路径从一个奇顶点出发，经过图中的边，最终到达另一个奇顶点

因此，原图 \(G\) 可以用 \(k\) 条不重复经过任何边的路径覆盖图中的所有边，即 \(G\) 是 \(k\) 笔画的

定义 6.4 哈密顿图

设 \(G=(V,E)\) 是一个无向图，如果 \(G\) 中存在一条经过每一个顶点且仅经过一次的闭迹（回路），则称 \(G\) 为哈密顿图，这样的闭迹称为哈密顿回路（哈密顿圈）

如果存在一条经过每一个顶点且仅经过一次的开迹，则称 \(G\) 为半哈密顿图，这样的开迹称为哈密顿路径（哈密顿路）

到目前为止，还没有一个非平凡的充分必要条件可以用来判定一个图是否为哈密顿图或半哈密顿图，这是图论中的一个重要未解问题

定理 6.4.1（必要条件）

若 \(G=(V,E)\) 是一个哈密顿图，则对于 \(G\) 的任意非空真子集 \(S \subset V\)，都有 \(\omega(G-S) \leq |S|\)，其中 \(\omega(G-S)\) 表示从图 \(G\) 中去掉顶点集 \(S\) 及其所有关联边后所得到的图的连通分支数

证明： 点击查看证明

证明：

设哈密顿回路 \(C\) 经过图 \(G\) 中的所有顶点，则对 \(V\) 的每一个非空真子集 \(S\) 有 \(\omega(C-S)\le S\)

因此，\(\omega(G-S) \leq \omega(C-S) \leq |S|\)

我们举出一个反例来说明该条件不是充分条件

考虑彼得森图

1

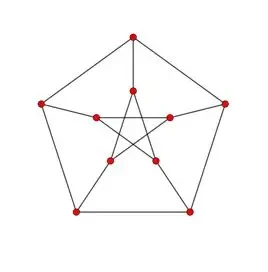
在图中删去任意一个或者两个顶点， 剩下的图都是连通的，删除三个顶点，最多只能得到有两个连通分支的图，删去四个顶点，最多只能得到有三个连通分支的图，删除五个或者五个以上的顶点，余下的顶点数不大于五，因此不能有五个以上的连通分支，因此对于彼得森图的任意非空真子集 \(S \subset V\)，都有 \(\omega(G-S) \leq |S|\)

下面证明彼得森图不是哈密顿图

证明： 点击查看证明

证明：

将彼得森图的边分为三类：

• 类1：连接外部大五边形的5条边
• 类2：连接内部小五角星的5条边
• 类3：连接内外顶点的5条边

如果这个图是哈密顿图，那么存在一条10条边组成的回路（10个顶点），该回路中的3类边有2条或4条（回到内圈或外圈的起点），否则无法回到起点形成回路

若由两条3类边，则外圈有4条边，内圈有4条边，无法构成回路（其他情况显然不成立）

若由四条3类边，则有一个还未连接的外圈顶点必有2条1类边与相邻外圈顶点相连，同理未连接的内圈顶点也必须有2条2类边与相邻的内圈顶点相连，此时无法构成回路

故彼得森图不是哈密顿图

接下来讨论一些哈密顿图的充分条件

先从 \(Dirac(1952)\) 给出的结果开始

定理 6.4.2 (充分条件)

设 \(G=(V,E)\) 是一个含有 \(n(n \geq 3)\) 个顶点的简单图，如果 \(G\) 中每个顶点的度至少为 \(\frac{n}{2}\)，即 \(\delta \ge \frac{n}{2}\) 则 \(G\) 是哈密顿图

证明： 点击查看证明

反证法：

假设 \(G\) 不是哈密顿图，且 \(G\) 是含有 \(n\) 个顶点的简单图，\(n \geq 3\)，且每个顶点的度至少为 \(\frac{n}{2}\)

由于 \(n \ge 3\) \(G\) 显然不能是完全图

设 \(u,v\) 是 \(G\) 的不相邻顶点，根据 \(G\) 中每个顶点的度至少为 \(\frac{n}{2}\)，则有

\[d(u) + d(v) \geq n\]

由于 \(u,v\) 不相邻，通过加边，可以使得 \(G+uv\) 变为哈密顿图，并且，由于 \(G\) 不是哈密顿图，所以 \(G+uv\) 的每个哈密顿回路必然包含边 \(uv\)，否则 \(G\) 就是哈密顿图

于是 \(G\) 中存在起点为 \(u\)，终点为 \(v\) 的路径 \(P\)，设 \(P\) 为 \(v_1v_2 \ldots v_n\)，其中 \(v_1=u\)，\(v_n=v\)

记

\[S = \{v_i | v_1v_{i+1} \in E(G), 2 \leq i \leq n-1\}\]

\[T = \{v_j | v_jv_n \in E(G), 2 \leq j \leq n-1\}\]

则 \(|S| = d(u)\)，\(|T| = d(v)\)，且 \(S,T \subseteq \{v_2,v_3,\ldots,v_{n-1}\}\)

由于 \(v_n \notin S \cup T\) ,则 \(|S \cup T| < n\) 并且 \(S \cap T\) 为空

否则如果不为空，设 \(v_k \in S \cap T\)，则 \(G\) 中存在回路 \(v_1v_2 \ldots v_kv_nv_{n-1} \ldots v_{k+1}v_1\)，与 \(G\) 不是哈密顿图矛盾

但是这里有 \(|S| + |T| = d(u) + d(v) \geq n\)，这与 \(|S \cup T|=|S| + |T| = d(u) + d(v) < n\) 矛盾

故 \(G\) 是哈密顿图

\(Bondy\) 和 \(Chvatal\) 在 \(1976\) 年基于上面的证明给出了哈密顿图的一个更有力的充分条件

定理 6.4.3 (充分条件)

设 \(G=(V,E)\) 是一个含有 \(n(n \geq 3)\) 个顶点的简单图，如果对于 \(G\) 中任意不相邻的两个顶点 \(u\) 和 \(v\)，都有 \(d(u) + d(v) \geq n\)，则 \(G\) 是哈密顿图

证明： 点击查看证明

反证法：

假设 \(G\) 不是哈密顿图，且 \(G\) 是含有 \(n\) 个顶点的简单图，\(n \geq 3\)，且对于 \(G\) 中任意不相邻的两个顶点 \(u\) 和 \(v\)，都有 \(d(u) + d(v) \geq n\)

由于 \(n \ge 3\) \(G\) 显然不能是完全图，设 \(u,v\) 是 \(G\) 的不相邻顶点，通过加边，可以使得 \(G+uv\) 变为哈密顿图，并且，由于 \(G\) 不是哈密顿图，所以 \(G+uv\) 的每个哈密顿回路必然包含边 \(uv\)，否则 \(G\) 就是哈密顿图

于是 \(G\) 中存在起点为 \(u\)，终点为 \(v\) 的路径 \(P\)，设 \(P\) 为 \(v_1v_2 \ldots v_n\)，其中 \(v_1=u\)，\(v_n=v\)

必存在点 \(v_i\) 和 \(v_1\) 相邻，且点 \(v_{i-1}\) 和 \(v_n\) 相邻，否则，若 \(v_1\) 与 \(v_{i_1},v_{i_2}, \ldots, v_{i_k}\) 相邻，则 \(v_n\) 必与 \(v_{i_1-1}, v_{i_2-1}, \ldots, v_{i_k-1}\) 不相邻，且这些点两两不同，则 \(d(v_1) \le k,d(v_n)\le n-k-1\)因此 \(d(v_1) + d(v_n) \leq n-1\)，与矛盾

从而存在回路 \(v_1v_2 \ldots v_{i-1}v_nv_{n-1} \ldots v_iv_1\)，与 \(G\) 不是哈密顿图矛盾

所以 \(G\) 是哈密顿图

当然，也可以用 定理 6.4.2 相似的过程来证明该定理，这里采用了不同的方式

显然的，可以从 定理 6.4.3 推出 定理 6.4.2

定义图的闭包：反复链接 \(G\) 中度之和至少为 \(n\) 的不相邻顶点对，直到不存在这样的顶点对为止，所得到的图称为 \(G\) 的闭包，记为 \(c(G)\)

定理 6.4.4（闭包的唯一性）

\(c(G)\) 是唯一的

证明： 点击查看证明

证明：

设 \(G_1\) 和 \(G_2\) 是 \(G\) 的两个闭包

假设 \(G_1 \neq G_2\)，则存在一对顶点 \(u,v\)，使得 \(u\) 和 \(v\) 在 \(G_1\) 中相邻，而在 \(G_2\) 中不相邻

由于 \(G_2\) 是 \(G\) 的闭包，\(u\) 和 \(v\) 在 \(G_2\) 中不相邻，说明在 \(G_2\) 中 \(d(u) + d(v) < n\)，同理，在 \(G_1\) 中 \(d(u) + d(v) < n\)

这与 \(u\) 和 \(v\) 在 \(G_1\) 中相邻矛盾

因此，\(c(G)\) 是唯一的

定理 6.4.5 (平凡的充分必要条件)

一个简单图是哈密顿图的充分必要条件是它的闭包是哈密顿图

证明： 点击查看证明

证明：(必要性)

设 \(G=(V,E)\) 是一个哈密顿图，存在一条经过每一个顶点且仅经过一次的闭迹 \(C\)

由于闭包 \(c(G)\) 是通过添加边得到的，因此闭迹 \(C\) 仍然存在于 \(c(G)\) 中

因此，\(c(G)\) 是一个哈密顿图

(充分性)

设 \(c(G)=(V,E')\) 是一个哈密顿图，存在一条经过每一个顶点且仅经过一次的闭迹 \(C\)

由于 \(E \subseteq E'\)，闭迹 \(C\) 中的边也存在于 \(G\) 中

因此，\(G\) 是一个哈密顿图

其实由闭包的构造过程可以知道这个结果是显然的

通过 定理 6.4.5，可以将判定一个图是否为哈密顿图的问题转化为判定其闭包是否为哈密顿图的问题

由此可以得到很多有趣的结果

定理 6.4.6

设图 \(G\) 是度序列为 \(d_1 \leq d_2 \leq \ldots \leq d_n\) 的简单图，如果存在不小于 \(\frac{n}{2}\) 的 \(m\) 使得 \(d_m \le m\) 和 \(d_{n-m} \le n-m\)，则 \(G\) 是哈密顿图

证明： 点击查看证明

记 \(d'_1 \leq d'_2 \leq \ldots \leq d'_n\) 为 \(c(G)\) 的度序列，假设 \(c(G)\) 不是完全图，设 \(u\) 和 \(v\) 是两个不相邻的顶点，且满足 \(d'(u) \le d'(v)\) 且 \(d'(u)+d'(v)\) 尽可能大，则 \(d'(u)+d'(v) < n\)，否则 \(u\) 和 \(v\) 应该相邻

记 \(S\) 为 \(V-\{v\}\) 中在 \(c(G)\) 中的不与 \(v\) 相邻的顶点集合，则 \(|S| = n-1-d'(v)\)，同理的定义 \(T\) 为 \(V-\{u\}\) 中在 \(c(G)\) 中不与 \(u\) 相邻的顶点集合，则 \(|T| = n-1-d'(u)\)

由于 \(u\) 和 \(v\) 的选择，\(S\) 中每个顶点的度不超过 \(d'(u)\)，\(T\) 中每个顶点的度不超过 \(d'(v)\)

则 \(c(G)\) 中至少有 \(m\) 个顶点，度最多为 \(m\)，并且至少有 \(n-m\) 个顶点，度最多为 \(n-m\)

由于 \(G\) 是 \(c(G)\) 的生成子图，上述结论对 \(G\) 也成立，所以与假设矛盾