集合与图论学习笔记10
定义
定义 10.1 网络
设连通无自环的带权有向图 \(G=(V,E)\),中有两个不同顶点 \(s\) 和 \(t\),且在弧集 \(E\) 上定义一个非负整数值函数 \(C\{c_{ij}\}\),称该有向图为网络,称该有向图为网络,记为 \(N(V,E,C)\)
其中:\(s\) 为发点,\(t\) 为收点,\(C\) 为容量函数,\(c_{ij}\) 为弧 \((i,j)\) 的容量,其他点称为中间点
定义 10.2 流
设 \(N(V,E,C)\) 是一个网络,\(f=\{f_{ij}\}\) 是定义在弧集 \(E\) 上的一个非负整数值函数,称 \(f\) 为网络 \(N\) 上的流
若 \(f\) 满足以下条件,则称 \(f\) 为网络 \(N\) 上的可行流,\(f_{ij}\) 称为弧 \((i,j)\) 上的流量,\(V_f\) 称为流 \(f\) 的值
容量限制条件:对于任意弧 \((i,j)\in E\),有 \(0\leq f_{ij}\leq c_{ij}\)
流量守恒条件:对于任意中间点 \(k\in V-\{s,t\}\),有 \(\sum_{i\in V}f_{ik}=\sum_{j\in V}f_{kj}\)
对于 \(s\) 和 \(t\),有 \(\sum_{i\in V}f_{ki}-\sum_{j\in V}f_{jk}=\begin{cases}V_f \quad k=s \\ -V_f \quad k=t\end{cases}\)
其中,如果没有弧 \((i,j)\),则约定 \(f_{ij}=0\) 和 \(c_{ij}=0\)
若 \(f_{ij}=c_{ij}\),则称弧 \((i,j)\) 是饱和的,否则称为未饱和的
定义 10.3 割,增广路
设 \(N(V,E,C)\) 是有一个发点 \(s\) 和收点 \(t\) 的网络,\(S\) 是 \(V\) 的一个子集,且 \(s\in S\),\(t\notin S\),则称 \((S,V-S)\) 为网络 \(N\) 的一个割,也记作 \((S,\overline{S})\)
若从网络 \(N\) 中删去任意一个割,则从 \(s\) 到 \(t\) 之间不存在有向路
割 \((S,\overline{S})\) 的容量定义为割中所有弧的容量之和,记为 \(C(S,\overline{S})\),即 \(C(S,\overline{S})=\sum_{i\in S, j\in\overline{S}}c_{ij}\)
顺向弧:弧 \((i,j)\) 满足 \(i\in S\) 且 \(j\in \overline{S}\)
反向弧:弧 \((i,j)\) 满足 \(i\in \overline{S}\) 且 \(j\in S\)
设 \(N(V,E,C)\) 是一个网络,\(f\) 是网络 \(N\) 上的一个可行流,对于 \(N\) 中的每一个路 \(P\)
定义一个整数 \(\iota(P)=\min_{e\in E(P)}\iota(e)\)
这里 \(\iota(a)=\begin{cases} c(a)-f(a) \quad a是P的顺向弧 \\ f(a) \quad \quad \quad a是P的反向弧 \end{cases}\)
显然 \(\iota(P)\) 是 \(P\) 上能增加的最大流量
若 \(\iota(P)=0\),则称路 \(P\) 为饱和路,否则为非饱和的
定义增广路为在残留网络 \(N_f\) 中,从发点 \(s\) 到收点 \(t\) 的一条非饱和路
定理 10.3.1
对于给定网络 \(N=(V,E,C)\),设 \(f\) 是一个可行流,则对于任意割 \((P,\overline{P})\),有 \(V_f\leq C(P,\overline{P})\),即流的值不大于任意割的容量
证明: 点击查看证明
证明:
根据流的平衡条件,对于发点 \(s\),有 \[ \sum_{i\in V}f_{si}-\sum_{j\in V}f_{js}=V_f \] 对于 \(P\) 中不是发点 \(s\) 的任意顶点 \(k\),有 \[ \sum_{i\in V}f_{ik}-\sum_{j\in V}f_{kj}=0 \] 将上述等式对 \(P\) 中的所有顶点求和,得到 \[ \sum_{k\in P}\left(\sum_{i\in V}f_{ki}-\sum_{j\in V}f_{jk}\right)=V_f \] 由于 \[ \sum_{k\in P,i\in P}f_{ki} = \sum_{k\in P,j\in P}f_{jk} \] 所以 \[ \sum_{k\in P,i\in \overline{P}}f_{ki}-\sum_{k\in P,j\in \overline{P}}f_{kj}=V_f \] 又因为 \(f_{ij}\geq 0\),所以 \[ V_f\leq \sum_{k\in P,i\in \overline{P}}f_{ki} \le \sum_{k\in P,i\in \overline{P}}c_{ki}=C(P,\overline{P}) \]
证明过程中有一个有用的结论:对于任何割 \((P,\overline{P})\),流的值等于从 \(P\) 流向 \(\overline{P}\) 的流量减去从 \(\overline{P}\) 流向 \(P\) 的流量,即 \(V_f=\sum_{k\in P,i\in \overline{P}}f_{ki}-\sum_{k\in P,j\in \overline{P}}f_{kj}\)
显然的,如果此时有流 \(V=C(P,\overline{P})\)
则 \(V\) 是最大流而 \((P,\overline{P})\) 是最小割
定理 10.3.2 最大流-最小割定理
设 \(N=(V,E,C)\) 是一个网络,\(f\) 是网络 \(N\) 上的一个可行流,则下列命题等价:
流 \(f\) 是网络 \(N\) 上的最大流
在残留网络 \(N_f\) 中不存在从发点 \(s\) 到收点 \(t\) 的增广路
存在网络 \(N\) 的一个最小割 \((S,\overline{S})\),使得流的值等于该割的容量,即 \(V_f=C(S,\overline{S})\)
证明: 点击查看证明
证明:
- \(\Rightarrow\) (2)
如果存在从发点 \(s\) 到收点 \(t\) 的增广路 \(P\),则可以通过增广路 \(P\) 增加流量,从而得到一个更大的流,矛盾
具体增加过程如下
设增广路 \(P\) 上的最小剩余容量为 \(\iota(P)\),则对于增广路 \(P\) 上的每一条顺向弧 \((i,j)\),有 \(f_{ij}=f_{ij}+\iota(P)\),对于增广路 \(P\) 上的每一条反向弧 \((i,j)\),有 \(f_{ij}=f_{ij}-\iota(P)\)
则流的值增加了 \(\iota(P)\),即 \(V_f=V_f+\iota(P)\)
这样的新流仍然是可行流,因为增广路 \(P\) 上的每一条顺向弧 \((i,j)\) 满足 \(f_{ij}+\iota(P)\leq c_{ij}\),每一条反向弧 \((i,j)\) 满足 \(f_{ij}-\iota(P)\geq 0\)
- \(\Rightarrow\) (3)
如果在残留网络 \(N_f\) 中不存在从发点 \(s\) 到收点 \(t\) 的增广路,则设 \(S\) 为所有能从发点 \(s\) 出发经过残留网络 \(N_f\) 中的路径到达的顶点构成的集合,\(\overline{S}=V-S\)
则 \((S,\overline{S})\) 是网络 \(N\) 的一个割
且对于任意弧 \((i,j)\),若 \(i\in S\) 且 \(j\in \overline{S}\),则在残留网络 \(N_f\) 中不存在弧 \((i,j)\),即 \(f_{ij}=c_{ij}\)
因此,有 \[ V_f=\sum_{k\in S,i\in \overline{S}}f_{ki}-\sum_{k\in S,j\in \overline{S}}f_{jk}=\sum_{k\in S,i\in \overline{S}}c_{ki}=C(S,\overline{S}) \]
- \(\Rightarrow\) (1)
如果存在网络 \(N\) 的一个割 \((S,\overline{S})\),使得流的值等于该割的容量,即 \(V_f=C(S,\overline{S})\),则根据定理 10.3.2 可知流 \(f\) 是网络 \(N\) 上的最大流
最大流的标号方法
标号方法分为两个过程,标号过程和增广过程,通过标号过程找到一条增广路,再由增广过程增加流量并去掉标号
标号过程:
- 给定初始流,不妨设初始流的值为 \(0\),给发点标号 \((-,\Delta s)\),其中 \(\Delta s=+\infty\)
- 选择一个已标号的顶点 \(i\),检查从顶点 \(i\) 出发的所有弧 \((i,j)\)
- 若 \((i,j)\) 是未饱和,即 \(f_{ij}<c_{ij}\),且顶点 \(j\) 未被标号,则给顶点 \(j\) 标号 \((i^+,\Delta j)\),其中 \(\Delta j=\min(\Delta i,c_{ij}-f_{ij})\),如果 \(f_{ij}=c_{ij}\) 不进行标号
- 若 \((j,i)\) 有 \(f_{ji}>0\),且顶点 \(j\) 未被标号,则给顶点 \(j\) 标号 \((i^-,\Delta j)\),其中 \(\Delta j=\min(\Delta i,f_{ji})\),如果 \(f_{ji}=0\) 不进行标号
- 重复上述过程,直到收点被标号或没有新的顶点可以标号为止
如果 \(t\) 被标号,则存在增广路,进行增广过程,否则算法结束,当前流即为最大流
增广过程:
如果在收点 \(t\) 处的标号为 \((k^+,\Delta t)\),则存在增广路 \(P\),从发点 \(s\) 出发经过标号回溯到收点 \(t\)
- 修改流 \(f\),对于增广路 \(P\) 上的每一条顺向弧 \((i,j)\),有 \(f_{ij}=f_{ij}+\Delta t\),对于增广路 \(P\) 上的每一条反向弧 \((i,j)\),有 \(f_{ij}=f_{ij}-\Delta t\),这样得到一个新的流 \(f'\),且有 \(V_{f'}=V_f+\Delta t\),然后去掉标号
- 对流 \(f'\) 重复标号过程和增广过程,直到收点 \(t\) 未被标号为止
此时得到的所有已标号的顶点构成集合 \(S\),则 \((S,\overline{S})\) 是网络 \(N\) 的一个最小割,且流的值等于该割的容量,即 \(V_f=C(S,\overline{S})\)
初始流量可以不为 \(0\),只要是一个可行流即可
每次标号时,可以选择任意一个已标号的顶点进行扩展
定义 10.4 匹配、完美匹配、近完美匹配、最大匹配
设无向图 \(G=(V,E)\),\(M\subseteq E\),若对于任意两条不同的边 \((u_1,v_1)\in M\) 和 \((u_2,v_2)\in M\),均有 \(u_1\neq u_2\) 且 \(u_1\neq v_2\) 且 \(v_1\neq u_2\) 且 \(v_1\neq v_2\),则称 \(M\) 为图 \(G\) 的一个匹配(独立边集)(对集)
一条边,如果出现在匹配 \(M\) 中,则称该边为匹配边,否则称为非匹配边
一个顶点,如果它是一条匹配边的端点,则称该顶点为匹配点,否则称为未匹配点
若匹配 \(M\) 覆盖了图 \(G\) 的所有顶点,则称 \(M\) 为图 \(G\) 的一个完美匹配
若匹配 \(M\) 覆盖了图 \(G\) 除一个顶点外的所有顶点,则称 \(M\) 为图 \(G\) 的一个近完美匹配
若图 \(G\) 上不存在包含更多边的匹配,则称匹配 \(M\) 为图 \(G\) 的一个最大匹配
由匹配边和非匹配边交错形成的路径称为交替路
始于未匹配点且终止于未匹配点的交替路称为增广路
这个增广路和上面的增广路的概念是不同的,注意区分
由于增广路的定义是始于未匹配点且终止于未匹配点,所以增广路的长度一定是奇数
如果将增广路上的匹配边和非匹配边翻转,那么它依然是交错路,且匹配数量 +1
寻找增广路并反转以增加匹配大小的过程称为增广,这相当于将匹配 \(M\) 和增广路 \(P\) 取对称差
定理 10.4.1
图 \(G\) 是一个二分图当且仅当 \(G\) 的每一个回路的长度均为偶数(如果 \(G\) 无回路,相当于任一回路的长度为 \(0\),\(0\) 视为偶数
证明: 点击查看证明
必要性
设 \(G\) 是二分图,\(G\) 中任意一个长度为 \(m\) 的回路 \(C=v_{i_0}v_{i_1}v_{i_2}v_{i_3}v_{i_4}...v_{i_{m-1}}v_{i_0}\)
\(G\) 的顶点集可分为两个不相交的子集 \(V_1\) 和 \(V_2\),且 \(C\) 上的任意一条边均连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点
则 \(v_{i_0}\in V_1\),\(v_{i_1}\in V_2\),\(v_{i_2}\in V_1\),\(v_{i_3}\in V_2\),依此类推有 \[ v_{i_k}\in\begin{cases}V_1 \quad k\text{ 为偶数} \\ V_2 \quad k\text{ 为奇数}\end{cases} \]
由于 \(v_{i_{m-1}}\in V_2\),所以 \(m-1\) 为奇数,即 \(m\) 为偶数
充分性
若 \(G\) 是连通图
按照下面的顶点集合来分顶点子集
\(V_1=\{v_i \mid v_i与v_0的距离为偶数\}\),\(V_2=V-V_1\)
下面证明 \(G\) 的任意一条边均连接 \(V_1\) 中的一个顶点和 \(V_2\) 中的一个顶点
设 \((u,v)\) 是 \(G\) 的一条边,若 \(u,v\in V_1\),则存在 \(v_0\) 到 \(u\) 的一条长度为偶数的路 \(P_1\),存在 \(v_0\) 到 \(v\) 的一条长度为偶数的路 \(P_2\)
则由 \(P_1\),\((u,v)\) 和 \(P_2\) 的反向路构成了一个长度为奇数的回路,与假设矛盾,另一边同理
若 \(G\) 是非连通图
则对 \(G\) 的每一个支路分别进行上述划分,得到的各个子集的并即为所求的两个顶点子集
定理 10.4.2 (Berge 引理)
设 \(G=(V,E)\) 是一个无向图,\(M\) 是 \(G\) 上的一个匹配,则 \(M\) 是 \(G\) 的一个最大匹配的充分必要条件是:在 \(G\) 中不存在相对于匹配 \(M\) 的增广路
证明: 点击查看证明
证明:
必要性
设 \(M\) 是图 \(G\) 的一个最大匹配,若 \(G\) 中存在相对于匹配 \(M\) 的增广路 \(P\),则将匹配 \(M\) 和增广路 \(P\) 取对称差,得到一个新的匹配 \(M'\),且 \(|M'|=|M|+1\),与 \(M\) 是最大匹配矛盾
充分性
设 \(M\) 不是图 \(G\) 的一个最大匹配,则存在一个匹配 \(M'\),使得 \(|M'|>|M|\)
考虑对称差 \(M\oplus M'\),图 \((V,M \oplus M')\) 的顶点度数是 0、1 或 2,因此图 \((V,M \oplus M')\) 的每个支路要么是一个回路,要么是一条路
度数为 \(2\) 的顶点相邻的两条边必定来自不同的匹配,所以这些回路中来自 \(M\) 和 \(M'\) 的边的数量是一样的
且至少存在一条路径中来自 \(M'\) 的边比来自 \(M\) 的边多一条,记该路径为 \(P\),\(P\) 的两端点均为未匹配点,因此 \(P\) 是相对于匹配 \(M\) 的增广路
记 \(G=(V,E)\) 是一个图,\(A\subseteq V\),则 \(A\) 的邻接点集定义为 \(N(A)=\{v\in V \mid (u,v)\in E, u\in A\}\)
定理 10.4.3 (Hall 定理)
设 \(G=(V_1\cup V_2,E)\) 是一个二分图,则 \(G\) 存在一个覆盖 \(V_1\) 的匹配的充分必要条件是:对于 \(V_1\) 的任意子集 \(A\),均有 \(|N(A)|\geq |A|\)
证明: 点击查看证明
证明:
必要性
设 \(G\) 存在一个覆盖 \(V_1\) 的匹配 \(M\),则对于 \(V_1\) 的任意子集 \(A\),由于匹配 \(M\) 覆盖了 \(A\) 中的所有顶点,所以 \(N(A)\) 中至少有 \(|A|\) 个顶点与 \(A\) 中的顶点相连,因此有 \(|N(A)|\geq |A|\)
充分性
设对于 \(V_1\) 的任意子集 \(A\),均有 \(|N(A)|\geq |A|\),若 \(G\) 中不存在一个覆盖 \(V_1\) 的匹配,则存在一个最大匹配 \(M\),使得 \(M\) 不覆盖 \(V_1\) 中的某个顶点,记该顶点为 \(u\)
则在图 \(G\) 中存在始于未匹配点 \(u\) 的交错树 ,设 \(S\) 是可通过某条交错路到达的所有位于 \(V_1\) 中的顶点构成的集合,\(T\) 是可通过某条交错路到达的所有位于 \(V_2\) 中的顶点构成的集合
则有 \(|T|=|S|-1\),且 \(N(S)=T\),因此有 \(|N(S)|=|T|=|S|-1<|S|\),与假设矛盾
根据hall 定理,二分图有一个有意思的性质
定理 10.4.4
如果二分图是 \(k\) 正则的,那么它有完美匹配
证明: 点击查看证明
证明:
设 \(G(X\cup Y,E)\)
对 \(X\) 有边数 \(|E| = \sum_{v \in X} d(v) = k|X|\),\(Y\) 同理
\(k|X| = k|Y|\),因为 \(k > 0\),所以 \(|X| = |Y|\)
设 \(S\) 是 \(X\) 的任意子集
设 \(E_S\) 为与 \(S\) 中顶点相连的边的集合,由于 \(G\) 是 \(k\)-正则的,从 \(S\) 发出的边总数为 \(|E_S| = k|S|\),这些边的另一端必然都在 \(S\) 的邻居集合 \(N(S)\) 中
因为 \(Y\) 中的顶点度数也是 \(k\),所以 \(N(S)\) 中的顶点最多能接受 \(k|N(S)|\) 条边
则 \(k|N(S)| \ge |E_S| = k|S|\),即 \(|N(S)| \ge |S|\)
根据 Hall 定理,图 \(G\) 存在一个覆盖 \(X\) 的匹配
又由于 \(|X| = |Y|\),所以该匹配实际上是一个完美匹配
记最大独立集 \(I\) 的顶点数为 \(G\) 的独立数,记为 \(\beta(G)\)
记最小点覆盖 \(C\) 的顶点数为 \(G\) 的覆盖数,记为 \(\alpha(G)\)
显然有 \(\beta(G)+\alpha(G)=|V|\)
这是因为
设 \(I\) 是图 \(G\) 的一个最大独立集,则 \(V-I\) 是图 \(G\) 的一个点覆盖,因此有 \(\alpha(G)\leq |V-I|=|V|-\beta(G)\),即 \(\beta(G)+\alpha(G)\leq |V|\)
设 \(C\) 是图 \(G\) 的一个最小点覆盖,则 \(V-C\) 是图 \(G\) 的一个独立集,因此有 \(\beta(G)\geq |V-C|=|V|-\alpha(G)\),即 \(\beta(G)+\alpha(G)\geq |V|\)
记最大匹配的大小为 \(\nu(G)\)
记最小边覆盖的大小为 \(\tau(G)\)
定理 10.4.5
若 \(\delta(G)\geq 1\),则有 \(\nu(G)+\tau(G)=|V|\)
证明: 点击查看证明
设 \(M\) 是图 \(G\) 的一个最大匹配,\(|M|=\nu(G)\),\(U\) 是 \(M\) 中所有匹配边的端点构成的顶点集,则有 \(|U|=2\nu(G)\)
设 \(W=V-U\),则 \(W\) 中的每个顶点均未被匹配边覆盖,且由于 \(\delta(G)\geq 1\),所以 \(W\) 中的每个顶点至少与 \(U\) 中的一个顶点相连
则在图 \(G\) 中存在一个边覆盖 \(C'\),使得 \(C'\supseteq M\),且 \(C'\) 覆盖了 \(W\) 中的所有顶点
则有 \(|C'|=|M|+|W|=\nu(G)+|V|-2\nu(G)=|V|-\nu(G)\),即 \(\tau(G)\leq |V|-\nu(G)\),从而有 \(\nu(G)+\tau(G)\leq |V|\)
设 \(C\) 是图 \(G\) 的一个最小边覆盖,\(|C|=\tau(G)\),设 \(H=G[C]\),设 \(D\) 是图 \(H\) 的一个最大匹配,则有 \(|D|\leq |C|=\tau(G)\)
记 \(U\) 为 \(D\) 中所有匹配边的端点构成的顶点集,则有 \(|U|=2|D|\)
设 \(W=V-U\),则 \(W\) 中的每个顶点均未被匹配边覆盖,且由于 \(\delta(G)\geq 1\),所以 \(W\) 中的每个顶点至少与 \(U\) 中的一个顶点相连
由于 \(D\) 是图 \(H\) 的一个最大匹配,所以 \(H[W]\) 中不存在匹配边
所以 \(|C|-|D|=|C-D| \ge |W|=|V|-2|D|\)
又因为 \(H\) 是 \(G\) 的子图,所以 \(D\) 也是 \(G\) 的一个匹配,因此有 \(|D|\leq \nu(G)\)
则有 \(\tau(G)-|D| \ge |V|-2|D|\),即 \(\tau(G)+|D| \ge |V|\),从而有 \(\tau(G)+\nu(G) \ge |V|\)
综上所述,有 \(\nu(G)+\tau(G)=|V|\)
定理 10.4.6 (Kőnig 定理)
设 \(G=(V_1\cup V_2,E)\) 是一个二分图,则 \(G\) 的最大匹配的大小等于 \(G\) 的最小点覆盖的大小
证明: 点击查看证明
证明:
设 \(M\) 是图 \(G\) 的一个最大匹配,\(|M|=k\)
由于 \(M\) 中的 \(k\) 条边互不相交(没有公共端点),对于 \(G\) 的任意点覆盖 \(C\),为了覆盖这 \(k\) 条边,\(C\) 必须包含每条匹配边中的至少一个端点。 因此,任意点覆盖的大小至少为 \(k\),即 \(\tau(G) \ge |M| = \nu(G)\)
设 \(U\) 是 \(M\) 中所有匹配边的端点构成的顶点集,则有 \(|U|=2k\)
设 \(W\) 是 \(V_1\) 中所有未被 \(M\) 覆盖的顶点构成的集合
用 \(Z\) 表示从 \(W\) 中的顶点出发,通过 \(M\)-交替路,即非匹配边、匹配边交替出现的路径)所能到达的所有顶点的集合,则有 \(W\subseteq Z\)
设 \(S=Z\cap V_1,T=Z\cap V_2\)
可以知道 \(T\) 中所有顶点均被 \(M\) 覆盖,否则存在一条增广路,与 \(M\) 是最大匹配矛盾
定义 \(C=(V_1-S)\cup T\),则 \(G\) 的每条边至少有一个端点在 \(C\) 中,因此 \(C\) 是图 \(G\) 的一个点覆盖
否则,设 \((u,v)\) 是图 \(G\) 的一条边,且 \(u\in S,v\in V_2-T\),
如果是匹配边,\(u\) 在交替路中,所以 \(v\) 也在交替路中,这与 \(v\in V_2-T\) 矛盾
如果是非匹配边,到达 \(u\) 的增广路以匹配边结束,此时 \((u,v)\) 可以加入到增广路中,这与 \(v\in V_2-T\) 矛盾
于是 \(C\) 是图 \(G\) 的一个点覆盖
并且有 \[ \begin{aligned} |C| &= |V_1 - S| + |T| \\ &= (|V_1| - |S|) + (|S| - |W|) \quad \text{(由性质2:} |T| = |S| - |W| \text{)} \\ &= |V_1| - |W| \end{aligned} \]
\(|V_1|\) 是 \(V_1\) 的总点数,\(|W|\) 是 \(V_1\) 中未被匹配的点数 两者的差值 \(|V_1| - |W|\) 正好等于 \(V_1\) 中被匹配覆盖的点数 因为 \(M\) 的每一条边恰好覆盖 \(V_1\) 中的一个点,所以被覆盖的点数等于匹配边数 \(k\) 即:\(|C| = k\)
因此,图 \(G\) 的最小点覆盖的大小不大于 \(k\)
综上所述,图 \(G\) 的最大匹配的大小等于图 \(G\) 的最小点覆盖的大小
定理 10.4.7
设 \(G=(V,E)\) 是一个二分图,则有 \(\beta(G)=\tau(G)\)
证明: 点击查看证明
根据 \(\beta(G)+\alpha(G)=|V|\) 和 \(\nu(G)+\tau(G)=|V|\),只需证明 \(\alpha(G)=\nu(G)\) 即可
即最大匹配的大小等于最小点覆盖的大小
因此有 \(\beta(G)=\tau(G)\)
定理 10.4.8(Tutte 定理)
设 \(G=(V,E)\) 是一个无向图,则 \(G\) 存在一个完美匹配的充分必要条件是:对于 \(G\) 的任意子集 \(S\subseteq V\),均有 \(o(G-S)\leq |S|\)
这里\(o(G-S)\) 表示子图 \(G-S\) 中顶点数量是奇数的连通分支的数量
证明: 点击查看证明
证明:显然只需要证明简单图即可
必要性
\(G\) 有完美匹配 \(M\),设 \(S\subseteq V\),并设 \(G_1,G_2,...,G_n\) 是 \(G-S\) 的奇分支,则每个 \(G_i\) 中有一个顶点与 \(S\) 中的某个顶点通过匹配边相连,因此有 \(o(G-S)=n\leq |S|\)
反之,假设对于 \(G\) 的任意子集 \(S\subseteq V\),均有 \(o(G-S)\leq |S|\),但没有完美匹配
设 \(G\) 是没有完美匹配的极大图 \(G^*\) 的生成子图,由于 \(G-S\) 是 \(G^*-S\) 的生成子图,所以有 \(o(G^*-S)\leq o(G-S)\)
所以 \(o(G^*-S)\leq |S|\) 对任意 \(S\subseteq V(G^*)\) 都成立
此时,让 \(S\) 为空集,则有 \(o(G^*)=0\),此时 \(v(G^*)\) 为偶数
用 \(U\) 表示 \(G^*\) 中度为 \(v-1\) 的顶点集,当 \(U=V\) 时,\(G^*\) 有完美匹配,矛盾
当 \(U\neq V\) 时,下面证明: \(G^*-U\) 是完全图的不相交的并图
假设不是, \(G^*-U\) 的某一个分支不是完全图,则在次分支存在顶点 \(x,y\) 和 \(z\) 使得\((x,y)\in E(G^*)\),\((y,z)\in E(G^*)\),但 \((x,z)\notin E(G^*)\)
此外,由于 \(y \notin u\),在 \(G^*-U\) 中存在顶点 \(w\),使得 \((y,w)\notin E(G^*)\)
由于 \(G^*\) 是不包含完美匹配的极大图,所以对于所有的 \(e \notin E(G^*)\),\(G^*+e\) 都有完美匹配,设 \(M_1\) 和 \(M_2\) 分别是 \(G^*+(x,z)\) 和 \(G^*+(y,w)\) 的完美匹配,并用 \(H\) 表示 \(M_1 \Delta M_2\) 导出的 \(G^* \cup \{xz,yw\}\) 的子图
由于 \(H\) 中每个顶点的度都是 \(2\),所以 \(H\) 是一些回路和偶数条路的并
进而由于沿着这些回路的 \(M_1\) 的边和 \(M_2\) 的边是交错的,所以这些回路都是偶圈,下面分两种情形讨论
情形1:\(xz\) 和 \(yw\) 在 \(H\) 的不同分支中,若 \(yw\) 在 \(H\) 的回路 \(C\) 中,则 \(M_1\) 在 \(C\) 中的边连同 \(M_2\) 不在 \(C\) 中的边一起组成了 \(G^*\) 的一个完美匹配,矛盾
情形2:\(xz\) 和 \(yw\) 在 \(H\) 的同一分支中,根据 \(x\) 和 \(z\) 的对称性,假定 \(x,y,w,z\) 依次出现在 \(C\) 中,于是 \(M_1\) 在 \(C\) 中的边连同 \(M_2\) 不在 \(C\) 中的边一起组成了 \(G^*\) 的一个完美匹配,矛盾
很容易得到下面的推论:
每个没有割边的 \(3\) 正则图都有一个完美匹配
证明: 点击查看证明
证明:
设 \(G\) 是没有割边的 \(3\) 正则图, \(S\) 是 \(V\) 的真子集,\(G_1,G_2,...,G_n\) 是 \(G-S\) 的奇分支,设 \(m_i\) 是一个端点在 \(S\) 一个端点在 \(G_i\) 的边的数量
则由于 \(G\) 是 \(3\) 正则图,所以有 \(\sum_{v\in V(G_i)d(v)}=3v(G_i)\) 且 \(\sum_{v\in S}d(v)=3|S|\)
\(m_i=\sum_{v\in V(G_i)}d(v)-2e(G)\) 是奇数,所以 \(m_i\geq 1\),又由于 \(G\) 没有割边,所以 \(m_i\geq 3\)
所以有 \(3n\leq \sum_{i=1}^{n}m_i=\sum_{v\in S}d(v)=3|S|\),即 \(n\leq |S|\)
因此,根据 Tutte 定理,图 \(G\) 有完美匹配
有割边的 \(3\) 正则图不一定有完美匹配,例如下图所示的图没有完美匹配
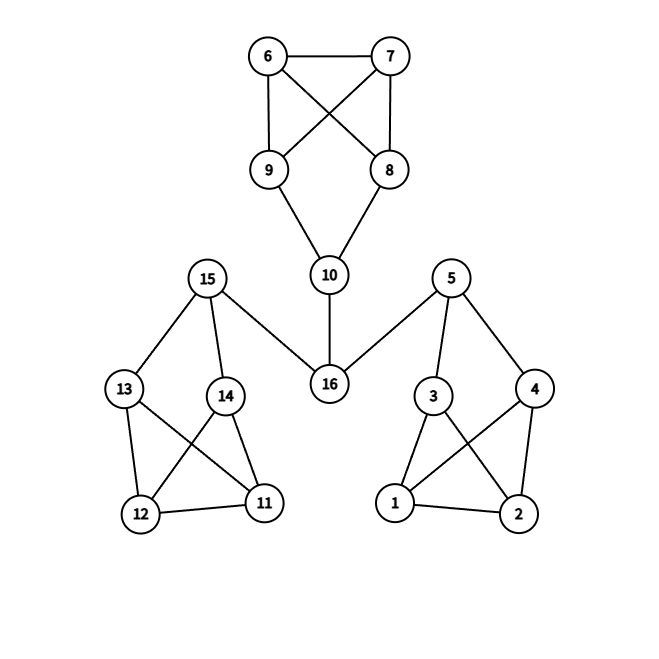
定理 10.4.9
对任意图 \(G\) ,点染色数 \(\chi(G) \ge \frac{|V|}{\beta(G)}\)
证明: 点击查看证明
证明:
根据独立集的定义,给一个独立集中的所有点染成同一种颜色是合法的染色方法
设图 \(G\) 有一个合法的 \(k\)-染色法,则图 \(G\) 的顶点集 \(V\) 可分为 \(k\) 个互不相交的独立子集 \(V_1,V_2,...,V_k\),即 \(V=V_1\cup V_2\cup ... \cup V_k\)
每一个颜色都是一个独立子集,因此有 \(|V_i|\leq \beta(G)\),\(i=1,2,...,k\)
则有 \(|V|=\sum|V_i| \le k\beta(G)\)
即 \(k \ge \frac{|V|}{\beta(G)}\),从而有 \(\chi(G) \ge \frac{|V|}{\beta(G)}\)
定理 10.4.10
对任意图 \(G\),记 \(\omega(G)\) 为 \(G\) 的最大团的大小,则有 \(\chi(G) \ge \omega(G)\)
证明: 点击查看证明
证明:
这是显然的。
如果图 \(G\) 有一个团 \(K\),则 \(K\) 中的任意两个顶点均相邻,因此在图 \(G\) 的任何合法染色中,\(K\) 中的每个顶点都必须被染成不同的颜色,所以图 \(G\) 的点染色数 \(\chi(G)\) 至少为 \(K\) 的顶点数,即 \(\chi(G) \ge \omega(G)\)
- Title: 集合与图论学习笔记10
- Author: exdoubled
- Created at : 2025-12-15 17:00:00
- Updated at : 2026-01-05 15:58:27
- Link: https://github.com/exdoubled/exdoubled.github.io.git/lssx/ls10/
- License: This work is licensed under CC BY-NC-SA 4.0.