线性表

线性表

exdoubled Lv4
  2025-09-17 17:00 2025-09-17 17:00 Created   2025-10-22 10:37:40 2025-10-22 10:37:40 Updated    3.2k Words  13 Mins  

特殊矩阵的储存

\(a_{ij}=a_{ji}\)

对称矩阵 \(A\) 的压缩存储

为节约存储，只存上三角矩阵或者下三角矩阵

下三角矩阵 \(j \le i\)，按行存储在一个一维数组 \(B\) 中，给出下标换算: \(B[k]\) 代表 \(A[i][j]\)

\[k=\frac{(i+1)\times i}{2}+j\]

反过来求利用\(0 \le j \le i\) 有：

\(\frac{(i+1)\times i}{2} \le k \le \frac{(i+1)\times i}{2}+i=\frac{(i+3)\times i}{2}\)

取左边不等式解得：

\[i = \lfloor \frac{-1+\sqrt{8k+1}}{2} \rfloor \]

\[j = k-\frac{(i+1)\times i}{2} \]

上三角矩阵 \(i < j\) ，按行存储在一个一维数组 \(B\) 中，给出下标换算: \(B[k]\) 代表 \(A[i][j]\)

\(k=\frac{i(2n-i+1)}{2}+(j-i)=\frac{i(2n-i-1)}{2}+j\)

反过来求利用\(0 \le j \le i\) 有：

\(\frac{i(2n-i-1)}{2} \le k \le \frac{i(2n-i-1)}{2}+i=\frac{i(2n-i+1)}{2}\)

三对角矩阵

为节约存储，只存非零位置，存储在一个一维数组 \(B\) 中，给出下标换算：\(B[k]\) 代表 \(A[i][j]\)

\[k=2i+j\]

注意到 \(j\) 只可能取到 \(i-1,i,i+1\) 三个值 并且 \(j > 0\)

在对角线上 \(i=j\) ，那么对角线元素有 \(k=3i\) ，对角线左边 \(k=3i-1\) 右边 \(k=3i+1\) 注意到此时 \(k\) 取值一定为 \(3\) 倍数，那么左侧模 \(3\) 余 \(-1\) ，右侧 模 \(3\) 余 \(1\) 显然此时加1取整后 \(i\) 的结果一定符合

\[i= \lfloor \frac{k+1}{3} \rfloor \]

\[j = k-2i\]

这种压缩（以至于所有线性递推）均带有 \(k = ai + j + b\) 的特征，所以可以解方程得到 \(a, b\)

带状矩阵采用类似三对角矩阵的储存方式 \(i,j,k\) 相关求法也和三对角矩阵一样

数组的动态定义方法

二维数组

1
2
3
4
int **a;
a=(int**)malloc(sizeof(int*) * rows);  // 定义一个一维指针数组
for(int i = 0; i < rows; ++i)
    a[i] = (int*) malloc(sizeof(int) * cols);   // 指针数组每一个元素均指向一个指针数组
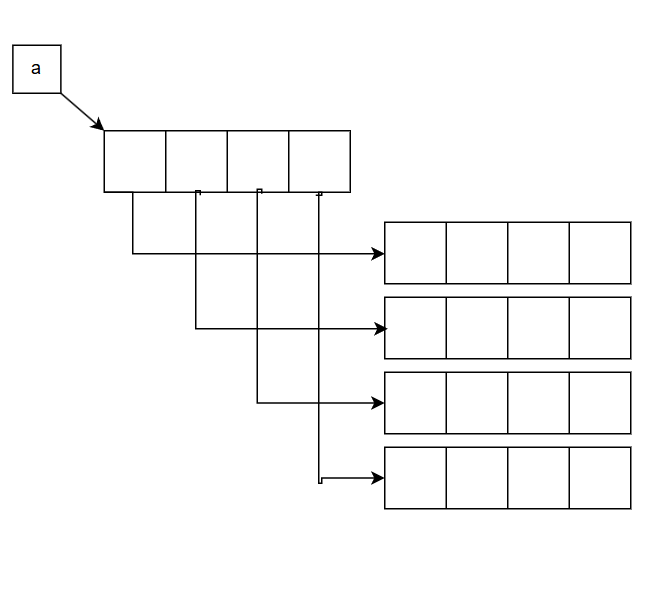
650X600/sjjg1-1.png

下三角矩阵

1
2
3
4
int **a;
a=(int**)malloc(sizeof(int*) * rows);  // 定义一个一维指针数组
for(int i = 0l i < rows; ++i)
    a[i] = (int*)malloc(sizeof(int) * (i+1));   // 指针数组每一个元素均指向一个指针数组
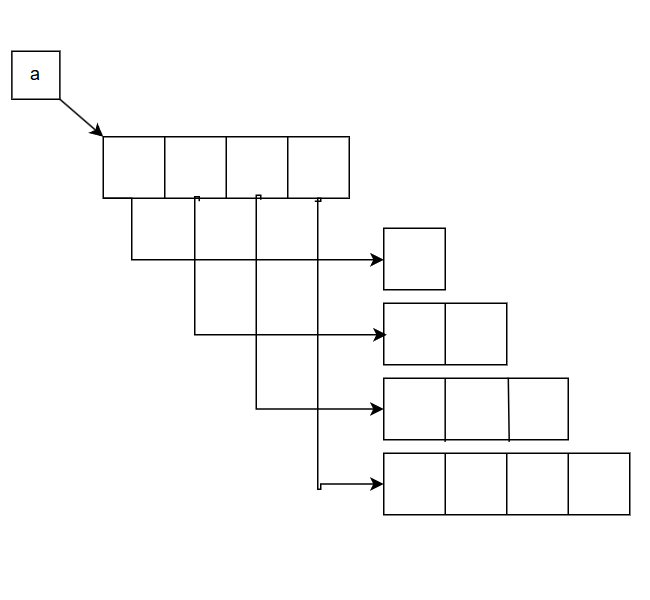
650X600/sjjg1-2.png

连续储存的定义

1
2
3
4
5
int **a;
a=(int**)malloc(sizeof(int*) * rows);  // 定义一个一维指针数组
int *b=(int**)malloc(sizeof(int*) * rows * (rows + 1) / 2);  // 压缩的数组
for(int i = 1, a[0] = b; i < rows; ++i)
    a[i] = a[i-1] + i;	// 每一个下标 i 一维指针数组含有 i+1 个元素

上三角矩阵

1
2
3
4
int **a;
a=(int**)malloc(sizeof(int*) * rows);  // 定义一个一维指针数组
for(int i = 0l i < rows; ++i)
    a[i] = (int*)malloc(sizeof(int) * (cols - i)) - i;   // 指针数组每一个元素均指向一个指针数组
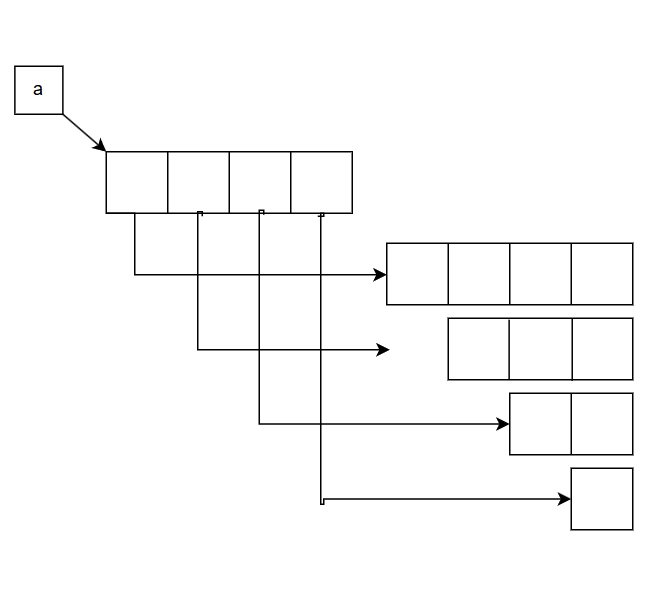
650X600/sjjg1-3.png

连续储存的定义

1
2
3
4
5
int **a;
a=(int**)malloc(sizeof(int*) * rows);  // 定义一个一维指针数组
int *b=(int**)malloc(sizeof(int*) * rows * (rows + 1) / 2);  // 压缩的数组
for(int i = 1, a[0] = b; i < rows; ++i)
    a[i] = a[i-1] + n - i;	// 每一个下标 i 一维指针数组含有 n - i + 1 个元素

稀疏矩阵

采用三元组的结构来表示稀疏矩阵

1
2
3
4
5
6
struct Node{
	int row;
	int col;
	int val;
};
vector<Node> v(n);

稀疏矩阵的转置

要求转置之后依然按照行为第一关键字，列为第二关键字升序存储。一个转置的做法是：对原矩阵从小到大枚举列号 \(k\)，每次对当前列号为 \(t\) 的所有元素进行转置。时间复杂度为 \(O(mt)\)，其 中 \(m\) 表示列数，\(t\) 表示三元组的数量。

快速转置算法

在不进行 \(O(n\log{n})\) 的排序的情况下 ，直接确定每个转置后元素在新三元表数组中的位置

考虑预处理统计出转置后的矩阵中每一行有多少元素，提前对这些元素分配存储空间,我们采用前缀和数组 $sum[i] $进行存储

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<Node> matrix(n);
vector<Node> ansMatrix(n);
vector<int> rowSize(cols, 0); // 辅助数组，统计各列非零元素的个数
vector<int> sum(cols, 0); // 辅助数组；统计转置后各元素位置 
for(int i = 0; i < n; ++i) rowSize[maxtrix[i].col]++;
for(int i = 1; i < cols; ++i) sum[i] = sum[i-1] + rowSize[i-1];
for(int i = 0; i < n; ++i){
    int j = sum[matrix[i].col];
    ansMatrix[j].row = maxrix[i].col;
    ansMatrix[j].col = maxrix[i].row;
    ansMatrix[j].val = maxrix[i].val;
    sum[maxtrix[i].col]++; // 存放位置后移
}

复杂度分析：

不妨设矩阵 \(n\times m\) 非零元素 \(t\)

生成辅助数组 \(rowSize\) 时间复杂度 \(O(t)\)

生成辅助数组 \(sum\) 时间复杂度 \(O(m)\)

三元组转置时间复杂度 \(O(t)\)

总时间复杂度 \(O(m+t)\)

稀疏矩阵的乘法

待整理

链表

数组可用 \(O(1)\) 访问任何元素， \(O(n)\) 的插入删除修改

链表适用于插入删除频繁的情形

但链表的速度不一定比数组快

普通的单向链表，循环链表，双向链表不再赘述

静态链表

使用数组实现链表的一种方式，比如并查集中可以使用

1
2
vector<int> father(n);
for(int i = 0; i < n; ++i) father[i] = i;

这样的方式来表示每个元素分别指向谁

增删改查其实与正常的链表逻辑无区别

静态链表适用于在不支持指针的高级程序设计语言中描述链表结构；或者适用于数据元素容量固定不变的场景（如操作系统的文件分区表 FAT） 。

块状链表

其实，分块是一种思想，而不是一种数据结构。

分块是一种很常用的思想，通过对原数据的适当划分，并在划分后的每一个块上预处理部分信息，从而较一般的暴力算法取得更优的时间复杂度。

块状链表结合了数组和链表的优点。块状链表可以看成一个链表每个链表结点中存储长度相等的小数组

下面给出一个有 \(9\) 个元素的块状链表的实现原理图

400X350/sjjg1-4.png

一般把长度为 \(n\) 的数组分为 \(\sqrt{n}\) 个结点，每个结点对应的数组大小为 \(\sqrt{n}\)

在最开始，不妨设每一个小数组长度均为 \(n\) ，\(n\) 越小，对其的插入删除就越快，\(n\) 雨打，遍历就越快

插入

  • 在末尾插入一个值

    找到最后一块小数组，在数组尾部插入，如果出现无法插入的情况，将该块分裂为大小为 $$ 和 $n-$ 的两块，然后在后一块插入

  • 在中间插入一个值

    通过每个块存储的当前块包含元素数量的信息得到 \(x\) 位置所对应的小数组结点，插入即可，若插入导致储存元素数量大于 \(n\) 则进行分裂

删除

删除指定位置 \(x\) 处的值

通过每个块存储的当前块包含元素数量的信息得到 \(x\) 位置所对应的小数组结点，删除即可

若删除该元素后导致结点元素少于 \(\lfloor \frac{n}{2}\rfloor\) 则从后一结点小数组中取出一些元素到当前节点中，如果这样进一步导致元素少于\(\lfloor \frac{n}{2}\rfloor\)，这时将两个结点合并即可

代码实现

结构定义如下

1
2
3
4
5
6
7
8
9
10
11
#define halfN  // n 的一半
#define SZ ((halfN << 1) + 2)  // 小数组最大的存储元素
struct node{
    node* next;
    int size,d[SZ]; // size 用来记录当前结点中存储的元素数量
    node(){size = 0; next = nullptr;}
    
    // 插入元素
    void push_back(int x){ d[size++] = x; }
}* head = nullptr;
int totnum = 0; // totnum 用来记录全局元素数量

块状链表包含以下几个函数

1
2
3
4
5
void split(node *p);	// 分裂节点
void merge(node *p);	// 合并节点
void ins(int x, int pos); // 插入元素
void del(int pos);		// 插入元素
int find(int pos);		// 查询元素
1
2
3
4
5
6
7
8
9
10
11
12
void split(node *p){
	// 如果当前节点元素数量大于n则进行分裂
	if(p->size >= (halfN << 1)){
		node* q = new node;	// 新建节点q
		for(int i = halfN; i < p->size; ++i) 
			q->push_back(q->d[i]); // 将p后一半加入q
		// 更新元素数量并且更新链表指针
		p->size = halfN;
		q->next = p->next;
		p->next = q;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void merge(node *p){
    node *q = p->next;
    if(q == nullptr) return;
    if(p->size + q->size <= (halfN << 1)){	// 如果元素之和小于n直接合并
        for(int i = 0; i < q->size; ++i)
            p->push_back(q->d[i]);	// q合并到p
        p->next = q->next;
        delete q;
        return;
    }
    int cnt = halfN - p->size;
    if(cnt <= 0) return;
    // 如果p的元素数量小于n/2，则从q中转移部分元素到p
    for(int i = 0; i < cnt; ++i) p->push_back(q->d[i]);
    for(int i = cnt; i < q->size; ++i) q->d[i-cnt] = q->d[i];
    q->size -= cnt; // 更新元素数量

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void ins(int x, int pos){
	node* p = head;
    // 判断是否在结尾插入
    if(pos > totnum++){
        while(p->next != nullptr) p = p->next;
        p->push_back(x);split(p);
        return;
    }
    int tot = 0; cnt = 0;
    // 找到 pos 对应的小数组
    for(tot = head->size; p != nullptr && tot < pos; p = p->next, tot+= p->size)
        cnt = pos - (tot - p->size) - 1;
    // 插入
    for(int i = p->size - 1; i >= cnt; --i)
        p->d[i+1] = p->d[i];
    p->d[cnt] = x;
    p->size++;
    split(p);
}
1
2
3
4
5
6
7
8
9
10
11
12
void del(int pos){
    node *p = head;
    int tot = 0, cnt = 0;
    for(tot = head->size; p != nullptr && tot < pos; p = p->next, tot += p->size)
        cnt = pos - (tot - p->size) - 1;
    // 删除
    for(int i = cnt; i < p->size; ++i)
        p->d[i] = p->d[i+1];
    p->size--;
    merge(p);
    totnum--;
}
1
2
3
4
5
6
int find(int pos){
	node* p = head;
	int tot = 0;
	for(tot = head->size; p != nullptr && tot < pos; p = p->next, tot += p->size);
	return p->d[pos - (tot - p->size) -1];
}

复杂度分析

不妨设小数组大小为 \(n\) ，总共元素为 \(m\)

  • 每次分裂的时间复杂度为 \(O(n)\)

  • 每次合并的时间复杂度为 \(O(n)\)

  • 每次插入的时间复杂度为 \(O(\frac{m}{n}+n)\)

  • 每次删除的时间复杂度为 \(O(\frac{m}{n}+n)\)

  • 每次查询的时间复杂度为 \(O(\frac{m}{n})\)

  • 空间复杂度为 \(O(m)\)

再回到原来的设法，当 \(n = O(\sqrt{m})\) 时，上述时间复杂度均为 \(O(\sqrt{m})\) 是比较好的，这就是我们最开始设个数的原因

STL中的 rope

STL 中的 \(rope\) 也起到块状链表的作用，它采用可持久化平衡树实现，可完成随机访问和插入、删除元素的操作。

时间复杂度 \(O(\log n)\)

1
2
#include <ext/rope>
using namespace __gnu_cxx;
操作作用
rope a初始化 rope（与 vector 等容器很相似）
a.push_back(x)在 a 的末尾添加元素 x
a.insert(pos, x)在 a 的 pos 个位置添加元素 x
a.erase(pos, x)在 a 的 pos 个位置删除 x 个元素
a.at(x) 或 a[x]访问 a 的第 x 个元素
a.length() 或 a.size()获取 a 的大小

约瑟夫问题的时间复杂度

用链表实现

使用循环链表实现，时间复杂度为 \(O(mn)\)

每次淘汰一个人就从链表中删去，显然时间复杂度为 \(O(mn)\) ，不再赘述

用数组实现

这里用循环数组，使用 vector<bool> visited(n) 来表示每个是否查询过 ，设每次数 \(m\) 个人

直接给出结论，时间复杂度 \(O(mn\log{n})\)

证明如下：

当已经查找 \(k\) 轮，现在还存活 \(r=n-k+1\) 个人，根据约瑟夫问题的规则，在一圈内，淘汰的人的分布几乎是均匀的，淘汰掉 \(n-1\) 个人转了若干圈，我们不妨把所有圈的均匀分布的间隔在每一圈均匀分布，此时，我们把淘汰的人的分布视为均匀的

视为均匀分布时，每个还存活的人相隔 \(\frac{n}{r}\) 个人，也就是说，每进行一次查找操作，程序进行了 \(\frac{n}{r}\) 次操作，查找 \(m\) 个人程序进行了 \(\frac{mn}{r}\) 次操作，则第 \(k\) 轮进行操作为 \(T_{k} = \frac{mn}{r}=\frac{mn}{n-k-1}\)

则时间复杂度为 ${k=1}{n-1}T_{k}=_{k=1}{n-1}=mn{k=1}^{n-1} $ ，这个式子趋于 \(mn(\ln{(n+1)} +\gamma)\)

也就是说，时间复杂度为 \(O(mn\log n)\) 或者说 $O(mnn) $

  • Title: 线性表
  • Author: exdoubled
  • Created at : 2025-09-17 17:00:00
  • Updated at : 2025-10-22 10:37:40
  • Link: https://github.com/exdoubled/exdoubled.github.io.git/sjjg/sjjg01/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
线性表
  1. 特殊矩阵的储存
  2. 数组的动态定义方法
  3. 稀疏矩阵
    1. 稀疏矩阵的转置
    2. 稀疏矩阵的乘法
  4. 链表
    1. 静态链表
    2. 块状链表
  5. 约瑟夫问题的时间复杂度
    1. 用链表实现
    2. 用数组实现