数字逻辑学习笔记01

数字逻辑学习笔记01

exdoubled Lv4
  2025-09-17 08:42 2025-09-17 08:42 Created   2025-10-22 10:38:30 2025-10-22 10:38:30 Updated    2.9k Words  13 Mins  

定义

简单的二进制数不再赘述

定义 1.1 各种十进制码

BCD 码（用二进制编码十进制数）

BCD 码是十进制数而不是二进制数

\(e.g\) : $(185) _ {10} = (0001 1000 0101) _ {BCD}=(10111001) _ {2} $

BCD 码的加法，像正常二进制做加法，若产生无效位，只需在无效位加上 0110 （加6）就得到正确的 BCD 码和一个进位，负数使用 BCD 的补码

8421码

十进制数BCD码（8421码）
00000
10001
20010
30011
40100
50101
60110
70111
81000
91001

2421码

十进制数2421码
00000
10001
20010
30011
40100
51011
61100
71101
81110
91111

余3码 （其实就是8421码加上0011）

十进制数余3码
00011
10100
20101
30110
40111
51000
61001
71010
81011
91100

84-2-1码

十进制数84-2-1码
00000
10111
20110
30101
40100
51011
61010
71001
81000
91111

2421 码和余 3 码和84-2-1码都是自补码，特性是其十进制数的反码通过将该码中的 0，1 互换直接得到，也就是说09、82、73、64互为反码

BCD 码不是自补码

定义 1.2 格雷码

格雷码的优点相比二进制数是从上一个数转换到下一个数时只有一位发生变换

格雷码

十进制数格雷码
00000
10001
20011
30010
40110
50111
60101
70100
81100
91101
101111
……

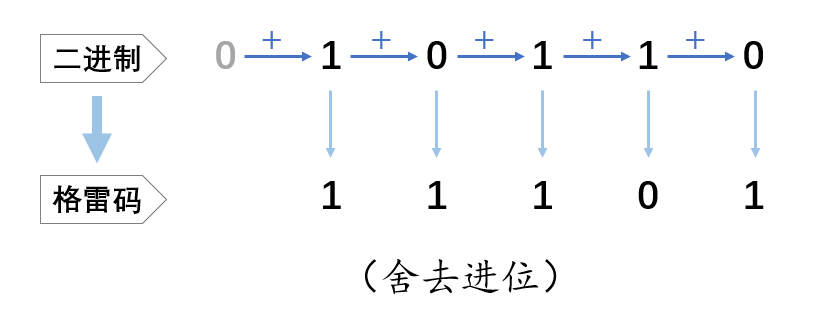
下面给出一个二进制数如何转换为格雷码

对二进制数 \((1000110101)_{2}\) ，最高位补位 \(0\) ， \((01000110101)\) ，从高位依次向低位做异或ans[i]=buffer[i]^buffer[i+1] 得到\((1100101111)\) ，格雷码转二进制先把首位放下来，从高位向低位交叉做异或，ans[i]=buffer[i]^ans[i+1]

823X314/szlj1-1.png
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<int> Decimal(n);
vector<int> Gray(n);


// 二进制转格雷码 
vector<int> GraytoDecimal(vector<int>& Decimal){
    int n = Decimal.size();
    vector<int> Gray(n);
    Gray[0] = Decimal[0];
    for(int i = 1; i < n; ++i) Gray[i] = Decimal[i-1] ^ Decimal[i];
    return Gray;

// 格雷码转二进制 
vector<int> GraytoDecimal(vector<int>& Gray){
    int n = Gray.size();
    vector<int> Decimal(n);
    Decimal[0] = Gray[0];
    for(int i = 1; i < n; ++i) Decimal[i] = Decimal[i-1] ^ Gray[i];
    return Decimal;
}

定义 1.3 奇偶校验码

在 码组 中增加一位，指使整个码组具有奇数个 1 或者偶数个 1 的信息

只具有发现出现奇数个错误的能力，无错误定位、纠正错误的能力。

\(e.g\)：

偶校验奇校验
10000010100000111000001
10101001101010001010100

定义 1.4 汉明码

汉明码可以纠错一个错误的数字

汉明码是在原来的数据插入 \(k\) 位数据作为校验位，原来 \(n\) 位变为 \(n+k\) 位 其中位数要满足

\[ n+k \le 2^{k}-1\]

这个不等式也叫汉明(Hamming) 不等式，编码规则如下

校验位位于码组索引位 \(2^{k}\) 的位置 \((k=0,1,2,...)\)，其余数位填数据位

校验位 \(P_{k}\) （位置 \(2^{k}\) ）校验 原码位置编号 的 二进制数 第 \(k\) 位是 \(1\) 的位，满足这一条件的位置的码的值全部异或得到校验值

  • \(P_{1}\)（位置1）覆盖位置1、3、5、7、9…（二进制最低位为1的位）
  • \(P_{2}\)（位置2）覆盖位置2、3、6、7、10…（二进制第二位为1的位）
  • \(P_{4}\)（位置4）覆盖位置4、5、6、7、12…（二进制第三位为1的位）

这里的校验可以为奇校验可以为偶校验

\(e.g\) ：1011 hamming编码为 0110011

下面给出纠错的步骤

1. 计算校验子（Syndrome）

  • 接收端收到码字后，重新计算每个校验位的奇偶性（与编码时规则相同）。
  • 对于每个校验位 \(P_{k}\)（位置 \(2^{k}\)），计算其覆盖组（所有位置编号二进制表示第k位为1的位）的异或值（偶校验预期为0）。
  • 若实际异或值不为0，则记录该校验位出错，记为1；否则为0。
  • 将所有校验位的校验结果按顺序（\(P_{1}，P_{2}，P_{3}\) …）组成一个二进制数（校验子S），其十进制值直接指出错误位置（从1开始编号）。

2. 定位错误位

  • 校验子 S 的十进制值即为错误位的位置（若为0则无错误）。
  • 例如：S=101（二进制）表示第5位错误；S=110 表示第6位错误。

\(e.g\)：

示例（接收码字：0110011，假设第5位出错变为0110111）

  1. 计算校验子：
    • \(P_{1}\)（覆盖位1,3,5,7）：异或位1+3+5+7 = 0⊕1⊕1⊕1=1（应为0，出错→记1）
    • \(P_{2}\)（覆盖位2,3,6,7）：异或位2+3+6+7 = 1⊕1⊕1⊕1=0（正确→记0）
    • \(P_{3}\)（覆盖位4,5,6,7）：异或位4+5+6+7 = 0⊕1⊕1⊕1=1（应为0，出错→记1）
  2. 校验子 S=\((P_{1}，P_{2}，P_{3})\)=101（二进制），十进制值为5。 ⇒ 错误发生在第5位。
  3. 纠正：翻转第5位（1→0），恢复正确码字 \(0110011\)

定义1.5 布尔代数

基本结构

布尔代数是一个六元组 \((B, +, \cdot, \bar{}, 0, 1)\)，其中：

  • \(B\) 是一个非空集合（称为载体集）

  • \(+\) 和 \(\cdot\) 是 \(B\) 上的二元运算（分别称为逻辑或和逻辑与）

  • \(\bar{}\) 是 \(B\) 上的一元运算（称为逻辑非或补运算）

  • \(0\) 和 \(1\) 是 \(B\) 中的两个特殊元素（分别称为零元和单位元）（实则一个是 \(+\) 的单位元，一个是 \(\cdot\) 的单位元）

公理系统

布尔代数满足以下公理：

  1. 交换律 \[a + b = b + a\] \[a \cdot b = b \cdot a\]
  2. 结合律 \[(a + b) + c = a + (b + c)\] \[(a \cdot b) \cdot c = a \cdot (b \cdot c)\]
  3. 分配律 \[a \cdot (b + c) = (a \cdot b) + (a \cdot c)\] \[a + (b \cdot c) = (a + b) \cdot (a + c)\]
  4. 同一律 \[a + 0 = a\] \[a \cdot 1 = a\]
  5. 补律 \[a + \bar{a} = 1\] \[a \cdot \bar{a} = 0\]

衍生性质

从上述公理可以推导出以下重要性质：

  1. 幂等律（重叠律） \[a + a = a\] \[a \cdot a = a\]
证明： 点击查看证明

$$ \[\begin{align*} a+a &= (a+a)\cdot 1 \\\\ &= (a+a)\cdot (a+\overline{a}) \\\\ &= a+a\cdot \overline{a} \\\\ &= a+0 \\\\ &= a \end{align*}\] $$

\[ \begin{align*} a \cdot a &= a\cdot a+0 \\\\ &= a\cdot a +a\cdot \overline{a} \\\\ &= a\cdot (a+\overline{a}) \\\\ &= a\cdot 1 \\\\ &= a \end{align*} \]

由上述证明我们知道这两个式子有对偶性，于是以下省略第二个式子的证明

  1. 有界律 \[a + 1 = 1\] \[a \cdot 0 = 0\]
证明： 点击查看证明

\[ \begin{align*} a+1 &= 1\cdot (a+1) \\\\ &= (\overline{a}+a)\cdot (a+1)\\\\ &= a+\overline{a}\cdot 1 \\\\ &= a+\overline{a} \\\\ &= 1 \end{align*} \]

  1. 吸收律 \[a + (a \cdot b) = a\] \[a \cdot (a + b) = a\]
    证明： 点击查看证明

    证明： \[ \begin{align*} a + (a \cdot b) &= a\cdot 1+a \cdot b \\\\ &= a\cdot (1+b) \\\\ &= a\cdot 1 \\\\ &= a \end{align*} \]

  2. 对合律（自反律） \[\overline{\overline{a}} = a\]
证明： 点击查看证明

证明：

\(\overline{a} + \overline{\overline{a}} = 1\)， \(\overline{a} \cdot\overline{\overline{a}} = 0\)

由 上述可知，\(\overline{\overline{a}}\) 是 \(\overline{a}\) 的补。
但补是唯一的，而 \(a\) 也是 \(\overline{a}\) 的补（因为 \(a + \overline{a} = 1\) 且 \(a \cdot \overline{a} = 0\)）。

  1. 德摩根律 \[\overline{a+b} = \overline{a} \cdot \overline{b}\] \[\overline{a \cdot b}= \overline{a} + \overline{b}\]
证明： 点击查看证明

证明 \(\overline{a} \cdot \overline{b}\) 是 \(a+b\) 的补元 \[ \begin{align*} (a+b)+(\overline{a}\cdot \overline{b}) &= a+b+(\overline{a}\cdot \overline{b})\\\\ &= a+[b+(\overline{a}\cdot \overline{b})]\\\\ &= a+[(b+ \overline{a})\cdot(b+ \overline{b})]\\\\ &= a+[(\overline{a}+ b)\cdot1] \\\\ &= a+\overline{a}+b \\\\ &= 1 + b \\\\ &= 1 \\\\ \end{align*} \]

  1. 消除律

\[ a+\overline{a}\cdot b = a+b\]

\[a\cdot (\overline{a}+b)=a\cdot b\]

证明： 点击查看证明

\[ \begin{align*} a+\overline{a}\cdot b &= a\cdot1+\overline{a}\cdot b \\\\ &= a\cdot(b+1)+\overline{a}\cdot b \\\\ &= a\cdot b + a\cdot 1 +\overline{a}\cdot b \\\\ &= (a+\overline{a})\cdot b + a \\\\ &= a + 1\cdot b \\\\ &= a+b \end{align*} \]

\[ \begin{align*} (a+b)\cdot (\overline{a}\cdot \overline{b}) &= (a\cdot \overline{a}\cdot \overline{b})+(b\cdot\overline{a}\cdot \overline{b}) \\\\ &= (0\cdot\overline{b})+(0\cdot\overline{a}) \\\\ &= 0+0 \\\\ &= 0 \\\\ \end{align*} \]

所以\(\overline{a} \cdot \overline{b}\)是 \(a+b\) 的补元 故\(\overline{a+b}\) = \(\overline{a} \cdot \overline{b}\)

示例

最简单的布尔代数是二元布尔代数 \((\{0, 1\}, +, \cdot, \bar{}, 0, 1)\)，其中：

  • \(0 + 0 = 0\), \(0 + 1 = 1\), \(1 + 0 = 1\), \(1 + 1 = 1\)
  • \(0 \cdot 0 = 0\), \(0 \cdot 1 = 0\), \(1 \cdot 0 = 0\), \(1 \cdot 1 = 1\)
  • \(\overline{0} = 1\), \(\overline{1} = 0\)

拓展

布尔代数和群的关系

这个二元布尔代数同构于伽罗瓦域 \(GF(2)\)

但不是所有布尔代数都同构于域，下面给出

定理：如果布尔代数 \((B, +, \cdot, \bar{}, 0, 1)\) 是一个域，那么 \(B\) 只能有2个元素。

证明： 点击查看证明

假设 \(B\) 是一个域，那么对于任意 \(a \in B\)，\(a \neq 0\)，存在 \(a^{-1}\) 使得 \(a \cdot a^{-1} = 1\)。

但在布尔代数中，有 \(a \cdot a = a\)，因此：\(a = a \cdot a = a \cdot a^{-1} = 1\)

这说明所有非零元素都等于1，因此：\(B = \\{0, 1\\}\)

主要原因是乘法逆元的要求不同

域 \((F, +, \cdot)\) 要求：

  • 每个非零元素 \(a \in F\) 都必须存在乘法逆元 \(a^{-1}\)，满足：\(a \cdot a^{-1} = 1\)

布尔代数 \((B, +, \cdot, \bar{}, 0, 1)\) 中：

  • 对于任意 \(a \in B\)，有幂等性：\(a \cdot a = a\)
  • 只有当 \(a = 1\) 时，才有 \(a \cdot a = 1\)（即 \(a^{-1} = a\)）
  • 对于 \(a \neq 0, 1\)，不存在 \(b \in B\) 使得 \(a \cdot b = 1\)

下面给出反例

设三元布尔代数 \(B = \{0, a, 1\}\)，其中 \(0 < a < 1\)，运算规则：

  • \(a \cdot a = a\)
  • 要满足 \(a \cdot b = 1\)，但 \(a \cdot 0 = 0\)，\(a \cdot a = a\)，\(a \cdot 1 = a\)
  • 不存在这样的 \(b\) 使得 \(a \cdot b = 1\)

布尔代数和环的关系

每一个布尔代数都可以自然地构成一个环，并且是一种特殊类型的环，称为布尔环。 布尔代数与布尔环是范畴等价的数学结构。

证明： 点击查看证明

下面用\((B, \lor, \land, ', 0, 1)\) 表示上面的\((B, +, \cdot, \bar{}, 0, 1)\) 以区分环上的运算

给定布尔代数 \((B, \lor, \land, ', 0, 1)\)，可定义对应的布尔环 \((B, +, \cdot, 0, 1)\)：

我们定义单位元不变

  • 环加法 \(a + b \equiv (a \land b') \lor (a' \land b)\)

  • 环乘法 \(a \cdot b \equiv a \land b\)

下面验证环公理

  1. \((B, +, 0)\) 构成阿贝尔群：

    • 封闭性：\(\forall a,b \in B, a+b \in B\)
    • 结合律：\((a + b) + c = a + (b + c)\)
    • 交换律：\(a + b = b + a\)
    • 单位元：\(a + 0 = a\)
    • 逆元：\(a + a = 0\)（每个元素都是自身的加法逆元）

  2. \((B, \cdot, 1)\) 构成幺半群：

    • 封闭性：\(\forall a,b \in B, a \cdot b \in B\)
    • 结合律：\((a \cdot b) \cdot c = a \cdot (b \cdot c)\)
    • 单位元：\(a \cdot 1 = 1 \cdot a = a\)

  3. 分配律： \[ a \cdot (b + c) = (a \cdot b) + (a \cdot c) \] \[ (a + b) \cdot c = (a \cdot c) + (b \cdot c) \]

  4. 特殊性质（布尔环特性）（幂等性）： \[ a \cdot a = a \land a = a \]

给定布尔环 \((R, +, \cdot, 0, 1)\)（满足 \(\forall a \in R, a^2 = a\)），可定义对应的布尔代数 \((R, \lor, \land, ', 0, 1)\)：

我们定义最小元0，最大元1

  • 布尔或：\(a \lor b \equiv a + b + a \cdot b\)
  • 布尔与：\(a \land b \equiv a \cdot b\)
  • 布尔非：\(a' \equiv 1 + a\)

下面验证布尔代数公理

  • 交换律、结合律、分配律
  • 同一律：\(a \lor 0 = a\)，\(a \land 1 = a\)
  • 补律：\(a \lor a' = 1\)，\(a \land a' = 0\)
  • 幂等律：\(a \lor a = a\)，\(a \land a = a\)

所以布尔环和布尔代数是等价的

  • Title: 数字逻辑学习笔记01
  • Author: exdoubled
  • Created at : 2025-09-17 08:42:00
  • Updated at : 2025-10-22 10:38:30
  • Link: https://github.com/exdoubled/exdoubled.github.io.git/szlj/szlj01/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
数字逻辑学习笔记01
  1. 定义
    1. 定义 1.1 各种十进制码
    2. 定义 1.2 格雷码
    3. 定义 1.3 奇偶校验码
    4. 定义 1.4 汉明码
    5. 定义1.5 布尔代数