数字逻辑学习笔记02

定义

定义 2.1 规范式

考虑二进制变量 \(x\) 和 \(y\) 的运算组合：

\(\overline{x}\overline{y}\)、\(\overline{x}y\)、\(x\overline{y}\)、\(xy\)，这 \(4\) 个与项的每一项称为最小项或者标准积。

\(\overline{x}+\overline{y}\)、\(\overline{x}+y\)、\(x+\overline{y}\)、\(x+y\)，这 \(4\) 个或项的每一项称为最大项或者标准和。

这是布尔函数的两个规范式

规定二进制数相应位 \(0\) 取反变量，相应位 \(1\) 取原变量

这样每一个最小项都对应一个二进制数 \(i\)，并把这个最小项记为 \(m_{i}\)

这样每一个最大项都对应一个二进制数 \(i\)，并把这个最大项记为 \(M_{i}\)

\(e.g.\)：

\[ f_{1}=\overline{x}\overline{y}z+x\overline{y}\overline{z}=m_{1}+m_{4}\]

\[f_{2}=(\overline{x}+\overline{y}+z)(x+y+z)=M_{6}M_{0}\]

任意一个布尔函数都可以表示为最小项之和或者最大项之积的形式

例如 \(F=A+\overline{B}C\)

可以表示成 \(F(A,B,C)=m_{1}+m_{4}+m_{5}+m_{6}+m_{7}=\Sigma(1,4,5,6,7)\)

例如 \(F=xy+\overline{x}z\)

可以表示为 \(F(x,y,z)=M_{0}M_{2}M_{4}M_{5}=\Pi(0,2,4,5)\)

容易知道 \(\overline{m_{i}}=M_{i}\)

定义 2.2 标准式

积之和式、和之积式是布尔函数的两种标准式

\(e.g.\)：\(F_{1}=\overline{y}+xy+\overline{x}y\overline{z}\) \(F_{2}=x(\overline{y}+z)(\overline{x}+y+\overline{z})\)

异或 \(\oplus\) 表示为 \(F=x\overline{y}+\overline{x}y=x\oplus y\)

同或表示为 \(F=xy+\overline{x}\overline{y}=\overline{x\oplus y}\)

给定布尔函数 \(F=xz+\overline{x}\overline{z}+\overline{x}y\)，分别使用与非门、反相器实现和或非门、反相器实现

\(F=xz+\overline{x}\overline{z}+\overline{x}y\)
\(F'=(\overline{xz})(\overline{\overline{x}\overline{z}})(\overline{\overline{x}y})\)
\(F=\overline{(\overline{xz})(\overline{\overline{x}\overline{z}})(\overline{\overline{x}y})}\)
\(F=(\overline{x}+\overline{z})(x+z)(x+\overline{y})\)
\(F'=\overline{(\overline{x}+\overline{z})}+\overline{(x+z)}+\overline{(x+\overline{y})}\)
\(F=\overline{\overline{(\overline{x}+\overline{z})}+\overline{(x+z)}+\overline{(x+\overline{y})}}\)
定义 2.3 卡诺图

卡诺图由一个个方格组成，每个方格代表布尔函数的一个最小项，由于任何布尔函数都能表示为最小项之和，那么将卡诺图中含有布尔函数最小项的这些方格圈在一起，根据画圈的图形就可以表示布尔函数。

卡诺图是标准式函数的图形化表示方法

详解可见：

四变量K-Map求解指南

卡诺图求解器 | 在线卡诺图化简工具

超过 \(4\) 个变量的卡诺图使用起来不方便，不予考虑

定义 2.4 质蕴含

在卡诺图选择相邻方格时，必须确保

这些被合并的方格能覆盖函数的所有最小项
表达式中的项数最少
没有冗余项（冗余项是指其最小项已被其他项覆盖）

质蕴涵是将卡诺图中最大可能数的相邻方格进行合并后获得的乘积项

如果方格中只被一个质蕴涵所包含，这样的质蕴涵就称为基本质蕴涵，不能从函数描述中将其移除

函数的质蕴涵可以通过合并卡诺图中所有可能的最大方格数得到

意味着：

卡诺图单个 \(1\) 如果不与其他 \(1\) 相邻，则表示他是一个质蕴涵
\(2\) 个相邻的 \(1\) 方格如果没有在一个四相邻的方格组中，形成一个质蕴涵
\(4\) 个相邻的 \(1\) 方格如果没有在一个八相邻的方格组中，形成一个质蕴涵
\(...\)

在卡诺图中， \(1\) 项代表函数式中的最小项，\(0\) 项代表函数式中的最大项

定义 2.5 无关项

无关项最小值（无关项）是逻辑值不确定的变量组合，对于这样的最小值，用 \(X\) 或 \(d\) 表示

表示不关心这个值是 \(0\) 还是 \(1\)

用卡诺图进行化简时：

化简为积之和在卡诺图上寻找 \(F=1\) 的项
化简为和之积在卡诺图上寻找 \(F=0\) 的项

可以通过两次取反法在卡诺图中将和之积化简为积之和

比如，化简最简与或式

先求 \(\overline{F}\) 的卡诺图，化简合并 \(0\) 项
再对 \(\overline{F}\) 取反得到答案

布尔函数可以用二级与非门实现，步骤如下

将函数化简为积之和式
画出表达式中至少含有两字母变量乘积项的与非门电路。每个乘积项的字母变量都是与非门的输入，这些项组成了第一级门电路
在第二级画出一个单独的门，该门采用了“与-非”或“非-或”图形符号，且其输入来自第一级门电路的输出
在第一级电路中，只有单字母输入的项需要一个非门，但如果这个字母是反变量，那么它可以直接连到第二级的与非门上

定义 2.6 奇函数

只有奇数个输入变量为 \(1\) 时，输出值为 \(1\)

三变量及三变量以上的 \(\oplus\) 运算都是奇函数

卡诺图可用来做运算，求反函数和对偶式

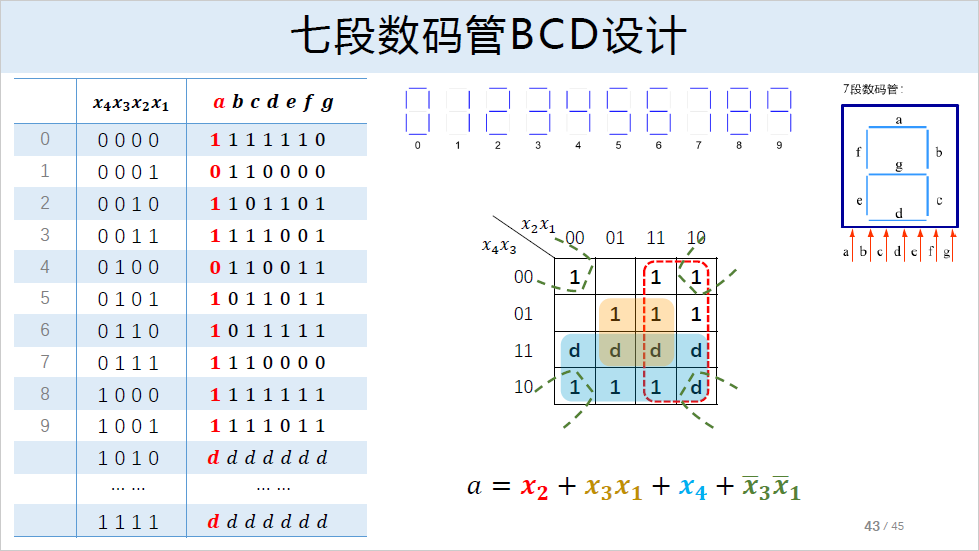
对于单输出函数化简只需符合要求的逻辑形式达到最小覆盖即可

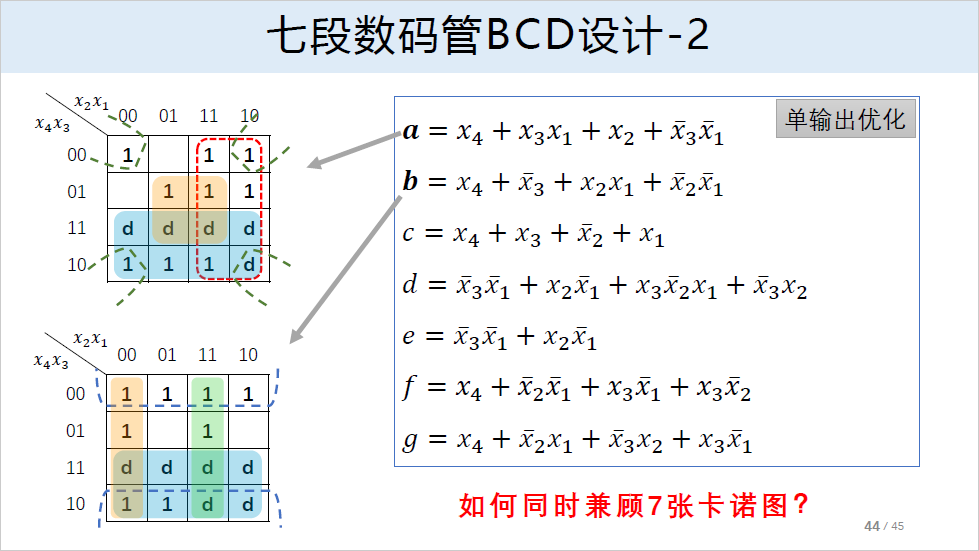
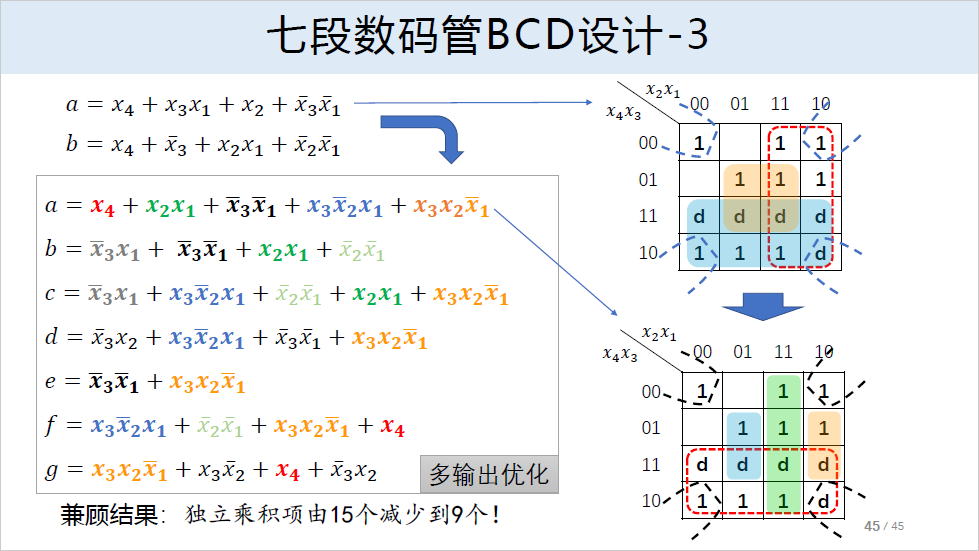
对于多输出函数由于存在各函数之间的相关性，需要考虑公共项

(´-ω-｀)