数字逻辑学习笔记04

锁存器

锁存器（Latch）是以信号电平（而不是信号转换）工作的存储元件

是一种对电平敏感的双稳态电路，具有 0，1 两种稳定状态

一旦状态被设置，就会保持该状态，直到输入信号改变

$SR$ 锁存器

$SR$ 锁存器是最基本的锁存器类型，由两个交叉连接的 $NOR$ 门或 $NAND$ 门组成。它有两个输入端 $S$（Set）（置位端）和 $R$（Reset）（复位端），以及两个输出端 $Q$ 和 $\overline{Q}$（$Q$ 的反相）

如何记忆？

当 $S=1$ 且 $R=0$ 时，锁存器被设置，$Q$ 变为 1
当 $S=0$ 且 $R=1$ 时，锁存器被重置，$Q$ 变为 0
当 $S=0$ 且 $R=0$ 时，锁存器保持其当前状态
当 $S=1$ 且 $R=1$ 时，通常被视为无效状态

Q: 为什么视为无效状态？
A: 因为两个输出端 $Q$ 和 $\overline{Q}$ 都会变为 0，这违反了互补关系，又两个或非门延迟不同，次态是 0 或 1 不可预测

特征方程

\[Q^{n+1} = S + \overline{R}Q^n\]

这样的电路具有 0，1 两种稳定状态，因此也称为双稳态电路（Bistable Multivibrator），一旦进入某一稳定状态，就会保持该状态，直到输入信号改变

约束条件

\[S+R=1\]

状态图

状态图反应了状态之间的转移关系

圆圈：稳定状态
有向线段：状态转移方向
- 起点：现态
- 终点：次态
- 触发条件

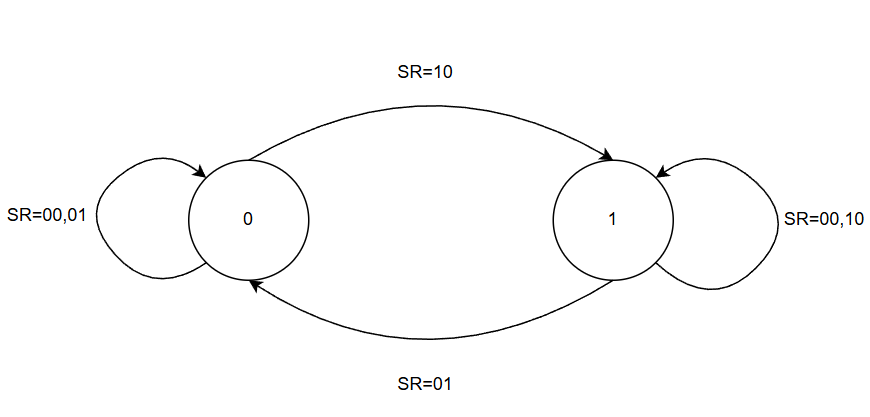
状态表

现态$Q^n$	SR=00	SR=01	SR=10	SR=11
0	0	0	1	d
1	1	0	1	d

带有使能的 $SR$ 锁存器

$Q^{n+1} = E(S + \overline{R}Q^n) + \overline{E}Q^n$

带有使能（Enable）输入的 $SR$ 锁存器只有在 En=1 时才响应 $S$ 和 $R$ 输入信号的变化

使能输入通常用于控制锁存器何时响应 $S$ 和 $R$ 输入信号

En	S	R	Q次态
0	d	d	保持
1	0	0	保持
1	0	1	Q=0，复位状态
1	1	0	Q=1，置位状态
1	1	1	不确定

$ $ 锁存器

$ $ 锁存器是另一种常见的锁存器类型，由两个交叉连接的 $NAND$ 门组成

它和 $SR$ 锁存器的工作原理类似，但输入信号是反相的

如何记忆？

当 $\overline{S}=0$ 且 $\overline{R}=1$ 时，锁存器被设置，$Q$ 变为 1
当 $\overline{S}=1$ 且 $\overline{R}=0$ 时，锁存器被重置，$Q$ 变为 0
当 $\overline{S}=1$ 且 $\overline{R}=1$ 时，锁存器保持其当前状态
当 $\overline{S}=0$ 且 $\overline{R}=0$ 时，通常被视为无效状态

特征方程

\[Q^{n+1} = \overline{\overline{S} + Q^n} \cdot \overline{\overline{R} + \overline{Q^n}}\]

约束条件

\[\overline{S}+\overline{R}=1\]

74 LS 279 ：四位 $ $ 锁存器

$ $ 锁存器是一个去抖电路

去抖电路（Debounce Circuit）是一种用于消除机械开关或按钮在切换过程中产生的抖动信号的电路。机械开关在打开或关闭时，触点可能会发生多次接触和断开，导致输出信号出现短暂的高频振荡，这种现象称为“抖动”。去抖电路通过滤除这些抖动信号，确保输出信号在开关状态稳定后才发生变化，从而提高系统的可靠性和稳定性

$D$ 锁存器

介绍门控 $D$ 锁存器（Data Latch），是一种常用的锁存器类型，它只有一个数据输入端 $D$ 和一个使能输入端 $E$，以及两个输出端 $Q$ 和 $\overline{Q}$

输出数据会随着输入数据的改变而改变，当使能信号无效时，一直保持在使能信号无效时的值，直到使能信号有效时为止

如何记忆？

当使能输入 $E=1$ 时，锁存器进入置位状态，将数据输入 $D$ 的值传递到输出端 $Q$
当使能输入 $E=0$ 时，锁存器进入复位状态，$Q$ 被置为 $0$

$Q^{n+1} = DE + \overline{E}Q^n$

状态图

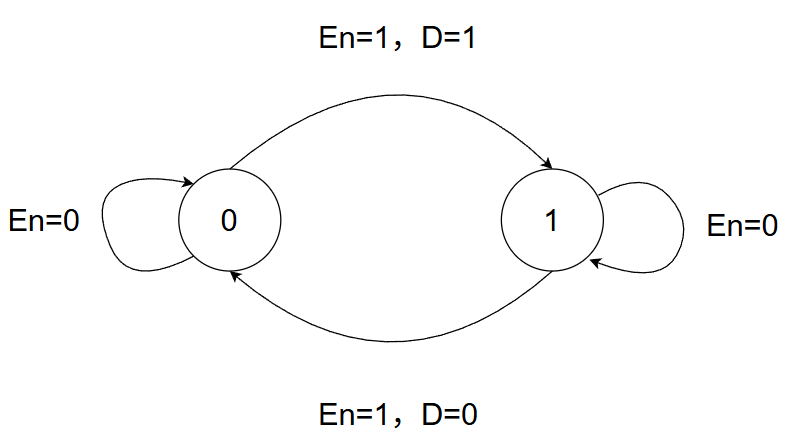
空翻：同一个 En 有效作用期间，锁存器状态发生两次或两次以上变化的现象

为了提高锁存器工作的可靠性，改用边沿触发方式，缩短时钟有效时间

触发器

边沿触发器：仅在时钟上升或下降沿时刻响应输入输入信号的触发器

仅在 $clk$ 某一约定跳变到来时，才接受输入信号

在 $clk=0 $或 $clk=1$ 期间输入信号变化不会引起输出状态的变化，不仅克服了空翻现象，且大大提高抗干扰能力

$SR$ 触发器

没有实际的产品，但是可以当作基础，实际是将门控 $SR$ 触发器的使能端 $E$ 换成了 $clk$

$clk$	$SR$	$ $	$Q^{n+1}$
×	$00$	$11$	$Q^{n}$
↑	$10$	$01$	$1$
↑	$01$	$10$	$0$
↑	$11$	$00$	$0$

$D$ 触发器

$D$ 触发器是一种常用的触发器类型，它只有一个数据输入端 $D$ 和一个时钟输入端 $CLK$，以及两个输出端 $Q$ 和 $\overline{Q}$

$D$ 触发器的 $S$ 和 $R$ 不会同时为高，这避免了 $SR$ 触发器不稳定的问题

当 $clk=1$ 时，有特征方程：

\[Q^{n+1}=D\]

可以通过三个 $D$ 锁存器构造下降沿 $D$ 触发器

用三个 $ $ 锁存器构造上升沿 $D$ 触发器

当 $clk=0$ 时， $\overline{S}=1,\overline{R}=1$，输出保持不变
当 $D=0,clk=1$ 时，$\overline{R}$ 变为 $0$，导致 $Q$ 变为 $0$
当 $D=1,clk=1$ 时，$\overline{S}$ 变为 $0$，导致 $Q$ 变为 $1$
当 $D=0 \rightarrow1,clk=1$ 时，$\overline{R}$ 保持 $0$ 不影响输出
当 $D=1 \rightarrow0,clk=1$ 时，$\overline{S}$ 保持 $0$ 不影响输出

带有 $reset$ 的 $D$ 触发器

异步：强制进入某状态

方框外有圆圈代表下降沿触发，否则代表上升沿触发

$JK$ 触发器

$JK$ 触发器是一种功能更强大的触发器类型，它有两个输入端 $J$ 和 $K$，以及一个时钟输入端 $clk$，和两个输出端 $Q$ 和 $\overline{Q}$

当 $clk=1$ 时

\[Q^{n+1}=J\overline{Q^{n}}+\overline{K}Q^n\]

$clk$	$J$	$K$	$Q^{n+1}$	$\overline{Q^{n+1}}$	说明
↑	$0$	$0$	$Q^{n}$	$\overline{Q^{n}}$	保持
↑	$1$	$0$	$1$	$0$	置$1$
↑	$0$	$1$	$0$	$1$	置$0$
↑	$1$	$1$	$\overline{Q^{n}}$	$Q^{n}$	翻转

$D$ 触发器构造 $JK$ 触发器

$JK$ 触发器可以通过在 $D$ 触发器的输入端添加逻辑门来实现

$T$ 触发器

$T$ 触发器常用来构成计数器

可以用 $D$ 触发器来构成

$D=T\overline{Q}+\overline{T}Q$

$T$	$Q(t+1)$	说明
$0$	$Q(t)$	保持
$1$	$\overline{Q}(t)$	翻转

$D$ 触发器构造 $T$ 触发器

$T$ 触发器可以通过在 $D$ 触发器的输入端添加一个 $XOR$ 门来实现

时序电路

同步时序电路：各个触发器的时钟脉冲相同。一般用触发器实现。在非时钟有效沿期间，触发器处于保持状态。

异步时序电路：各个触发器的时钟脉冲不同。既可用触发器、也可用锁存器。电路状态的翻转有先有后。

同步时序电路中时钟偏移

从同一时钟源出发的时钟脉冲，通过不同路径到达每个触发器的时间不同而产生的偏差

解决方法有增加缓冲器、对称布局等

有限状态机

有限状态机对有限内部状态相互转换的系统进行建模

状态机表示方法：状态图、状态表、流程图。三者等价

摩尔(Moore)状态机

输出只与当前状态有关，与输入无关

米里(Mealy)状态机

输出不仅与当前状态有关，还与输入有关

同一系统，既可以用摩尔模型描述，也可以用米里模型描述

状态图的直接构图法

先假定一个初态
每加入一个输入，就可以确定一个次态，这个次态可能是现态本身，也可能是已有的状态，也可能是新增状态
重复上一个步骤，直到每一个现态向其次态转换都被考虑，且不增加新状态

状态化简

在时序电路中，减少触发器数目的过程

化简原则：电路的输入输出关系保持不变

副作用：可能会使电路中增加更多组合逻辑

当对当前状态化简时，使用状态表比状态图方便

对所有的可能输入、输出都相同，且电路的次态相同或等效

等效状态具有传递性

时序逻辑设计

如果电路有 $m$ 个状态，就需要 $n$ 位二进制，$2^n>m$

状态编码：要利于函数的化简

原则：

次态相同，现态相邻
同一现态，次态相邻
输出相同，现态相邻

编码方案数：$\frac{2^n!}{(2^n-m)!}$

#include <iostream>
#include <vector>
#include <queue>

using namespace std;
using ll = long long;
using ld = long double;


struct Edge {
    int v;
    ll l, s;
};

vector<vector<Edge>> g;
vector<int> key;


bool dfsCycle(int u) {
    key[u] = 1;
    for (auto e : g[u]) {
        int v = e.v;
        if (key[v] == 0) {
            if (dfsCycle(v)) return true;
        } else if (key[v] == 1) return true;

    }
    key[u] = 2;
    return false;
}

bool hasNegativeCycle(int n, ld M) {
    vector<ld> dist(n + 1, 0.0L);
    vector<int> inq(n + 1, 1), cnt(n + 1, 0);
    queue<int> q;
    for (int i = 1; i <= n; ++i) q.push(i);

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        inq[u] = 0;
        for (const auto &e : g[u]) {
            ld w = (ld)e.s - M * (ld)e.l;
            if (dist[e.v] > dist[u] + w + 1e-18L) {
                dist[e.v] = dist[u] + w;
                if (!inq[e.v]) {
                    inq[e.v] = 1;
                    q.push(e.v);
                    if (++cnt[e.v] > n) return true;
                }
            }
        }
    }
    return false;
}

void solve() {
    int n,m;
    cin >> n >> m;
    g.assign(n+1, {});
    for (int i = 0; i < m; ++i) {
        int u, v;
        ll l, s;
        cin >> u >> v >> l >> s;
        g[u].push_back(Edge{v, l, s});
    }

    key.assign(n+1,0);
    bool hasCycle = false;
    for (int i = 1; i <= n && !hasCycle; ++i) {
        if (key[i] == 0 && dfsCycle(i)) hasCycle = true;
    }
    if (!hasCycle) {
        cout << "A+\n";
        return;
    }


    ld lo = 0.0L, hi = 1e9L;
    for (int it = 0; it < 80; ++it) {
        ld mid = (lo + hi) / 2.0L;
        if (hasNegativeCycle(n, mid)) hi = mid;
        else lo = mid;
    }
    ld iq = hi;
    if (iq >= 140.0L) cout << "A+\n";
    else if (iq >= 120.0L) cout << "A\n";
    else if (iq >= 110.0L) cout <<  "B\n";
    else if (iq >= 90.0L)  cout << "C\n";
    else if (iq >= 70.0L)  cout <<  "D\n";
    else cout <<  "E\n";
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

\(clk\)	\(SR\)	$ $	\(Q^{n+1}\)
×	\(00\)	\(11\)	\(Q^{n}\)
↑	\(10\)	\(01\)	\(1\)
↑	\(01\)	\(10\)	\(0\)
↑	\(11\)	\(00\)	\(0\)

\(clk\)	\(J\)	\(K\)	\(Q^{n+1}\)	\(\overline{Q^{n+1}}\)	说明
↑	\(0\)	\(0\)	\(Q^{n}\)	\(\overline{Q^{n}}\)	保持
↑	\(1\)	\(0\)	\(1\)	\(0\)	置\(1\)
↑	\(0\)	\(1\)	\(0\)	\(1\)	置\(0\)
↑	\(1\)	\(1\)	\(\overline{Q^{n}}\)	\(Q^{n}\)	翻转

\(T\)	\(Q(t+1)\)	说明
\(0\)	\(Q(t)\)	保持
\(1\)	\(\overline{Q}(t)\)	翻转

(´-ω-｀)

数字逻辑学习笔记04

锁存器

\(SR\) 锁存器

$ $ 锁存器

\(D\) 锁存器

触发器

\(SR\) 触发器

\(D\) 触发器

\(JK\) 触发器

\(T\) 触发器

时序电路

有限状态机

摩尔(Moore)状态机

米里(Mealy)状态机

状态图的直接构图法

状态化简

时序逻辑设计